1.5.3 Maximum likelihood estimate of parameters

SYLLABUS Previous: 1.5.2 Moving averages: UWMA, Up: 1.5 Historical data and Next: 1.6 Computer quiz

1.5.3 Maximum likelihood estimate of parameters $\spadesuit$

[ SLIDE method - lambda - GARCH - forecast - run || VIDEO modem - LAN - DSL ]

Even if a model provides an accurate description of statistical data, it is important that occasional outliners be discarded from the fit. Instead of minimizing a residual between the model and all the data points, a maximum likelyhood estimation therefore aims at maximizing the probability that the model reproduces most, but not all the data points. For example, imagine a coin thrown five times into the air with, as an outcome 1 heads and 4 tails. The maximum likelyhood estimate of observing the sequence in that order can be calculated by maximizing the probability of the observation max[p(1-p)⁴]: setting the derivative equal to zero (1-p)⁴-4p(1-p)³=0, this yields p=0.2 as expected.
The same method can be applied when the market increments are normally distributed with a variance n_i=s_i² that is allowed to change over time. The maximum likelyhood of reproducing the market data in that order can then be calculated from the optimum

$\displaystyle \mathrm{max}\prod_{i=1}^m \left[ \frac{1}{\sqrt{2\pi\nu_i}}\exp\l... ...}(\chi), \quad \chi=\sum_{i=1}^m \left[ \ln(\nu_i) +\frac{u_i^2}{\nu_i} \right]$

(1.5.3#eq.1)

where the second expression has been obtained after realizing that the maximum of a quantity coincides with the maximum of its logarithm and the minimum of the opposite. Model parameters, such as l in n_i(l) for the EWMA model of the volatility (1.5.2#eq.5) are then calculated to maximize the likelihood of reproducing the data by setting the first derivative equal to zero dC/dl=0 and keeping the second derivative positive d²C/dl²>0. Even if several parameters have to be determined p_i,p_jÎ {a,b,...} the gradient and the Hessian can be conveniently calculated from a sequence

$\begin{subequations}\begin{alignat}{2} \frac{\partial \chi_n }{\partial p_i} &= ... ...\left(\frac{\partial \nu_n}{\partial p_j}\right) \end{alignat}\end{subequations}$

where the last approximation guarantees a positive diagonal (i=j) when using a Levenberg-Marquardt solver to locate the zeros of the non-linear function (1.5.3#eq.2a).
The EWMA model (1.5.2#eq.5) has one free parameter (p₁)l) that can be estimated anew after every trading day. The link below shows how the derivatives of the variance

$\begin{subequations}\begin{alignat}{2} \nu_n &= \lambda\nu_{n-1} +(1-\lambda) u_... ...2} +2\frac{\partial\nu_{n-1}}{\partial\lambda} & \end{alignat}\end{subequations}$

are updated before the Levenberg-Marquardt algorithm [18] is used to calculate the parameter as a zero of the non-linear likelihood derivative (1.5.3#eq.2a). Note that a more simple Newton algorithm for finding roots of scalar variables could have been used instead, but would be insufficient when more than one parameter has to be estimated.
The GARCH(1,1) model (1.5.2#eq.6) has three free parameters (p₁)b, p₂)a p₃)w) and requires the evaluation of the gradient

$\begin{subequations}\begin{alignat}{2} \nu_n &= \omega+\beta\nu_{n-1}+\alpha u_{... ...eta\frac{\partial\nu_{n-1}}{\partial\omega} + 1& \end{alignat}\end{subequations}$

Maximum likelyhood of the fit is achieved when all three components of the gradient are equal to zero, which defines the parameters using the same Levenberg-Marquardt algorithm to locate the zeros of (1.5.3#eq.2a).
The MKTSolution applet below illustrates how the estimation works for the price history of the Asea Brown Boveri share during 2001-2003, rapidly switching between different regimes that are rather stable to produce the final estimate of l=0.8891 for the EWMA model, and w=0.000162, a=0.03134, b=0.8000 for the GARCH(1,1) model.

Market data: EWMA and GARCH(1,1) parameter estimation

Compare the volatility of the ABB share obtained for the EWMA model with a constant 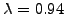$\lambda=0.94$ or a maximum likelihood estimate of the parameter. Identify regimes where the estimate may be above or below 0.94.
Study the volatility obtained for the GARCH(1,1) model, checking whether it is possible to define a long-term average, evaluate the impact of recent events and tell how quickly they are forgotten.
Which value of the volatility would you use to predict the financial risk in the year following this sequence?

It turns out parameter estimation is an important but rather delicate taskin the sense that the result depends strongly on the choice of the time window and abrupt changes in the price history can lead to significant changes in the model. This is of course what the estimation is meant to do, but it is important to make sure that the values that are predicted are not only mathematically correct, but also financially meaningful.
Knowing the present value of the variance model parameters, it is possible to forecast the financial risk into the future. Substituting the long term average w=V(1-a-b) into the recursive definition (1.5.2#eq.6), exercise 1.11 shows that the expected value k days into the future becomes

$\displaystyle E[\sigma_{n+k}^2]=V + (\alpha+\beta)^k(\sigma_n^2 -V)$

(1.5.3#eq.5)

For the EWMA model a+b=1) so that the expected future variance is equal to the present value. For the GARCH model, a+b<1) the second term decreases in importance for an increasing number of days k, showing that the variance exhibits a mean reversion towards the level V at a rate 1-a-b) . An average of the variance term structure

$\displaystyle \bar{\sigma^2}=\frac{1}{N}\sum_{k=0}^N E[\sigma_{n+k}^2]$

(1.5.3#eq.6)

is then generally used to parametrize option pricing models.

SYLLABUS Previous: 1.5.2 Moving averages: UWMA, Up: 1.5 Historical data and Next: 1.6 Computer quiz