4.4.1 Naive implementation using financial variables


 SYLLABUS Previous: 4.4 Methods for European
Up: 4.4 Methods for European
Next: 4.4.2 Improved scheme using
SYLLABUS Previous: 4.4 Methods for European
Up: 4.4 Methods for European
Next: 4.4.2 Improved scheme using
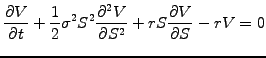 |
double timeStep = runData.getParamValue("TimeStep");
double strike = runData.getParamValue("StrikePrice");
double rate = runData.getParamValue("SpotRate");
double divid = runData.getParamValue("Dividend");
double sigma = runData.getParamValue("Volatility");
double sigmaSq = sigma*sigma;
for (int j=1; j<n; j++) { //Explicit 2 levels
fp[j]=f[j+1]* 0.5*timeStep*(sigmaSq*j*j + rate*j)
+f[j ]*(1.0-timeStep*(sigmaSq*j*j + rate ))
+f[j-1]* 0.5*timeStep*(sigmaSq*j*j - rate*j);
} //Boundary condition
if (isCall) { fp[0]=0; fp[n]=n*dx[0] -strike*Math.exp(-rate*time);
} else if(isPut) { fp[0]=strike*Math.exp(-rate*time); fp[n]=fp[n-1];
} else { fp[0]=fp[1]; fp[n]=fp[n-1]; }
showing clearly how the option values at the new time level fp[j]
are explicitly calculated in terms of the old values f[j].
To limit the required size of the simulation domain around the strike price,
it is marginally better to replace the Dirichlet condition fp[n]=0
with a Neumann condition fp[n]=fp[n-1].
This is what has been used above for the put option and in the default,
so as to accommodate in a simple manner for more general payoffs from
binary options.
The VMARKET applet below shows an application
using this very simple model.
SYLLABUS Previous: 4.4 Methods for European Up: 4.4 Methods for European Next: 4.4.2 Improved scheme using