2.1.1 Shares and market indices

SYLLABUS Previous: 2.1 The stock market Up: 2.1 The stock market Next: 2.1.2 Forward contract and

2.1.1 Shares and market indices

[ SLIDE random walk - log-normal - Lévy - drifts || VIDEO modem - LAN - DSL ]

Small companies generally start developing a product using private resources and sometimes a limited amount of venture capital. If all goes well, they may under circumstance decide to go to the stock market for the quest of new capital, which will allow them to grow more rapidly than what they could achieve by simply re-investing their own earnings.

Investment banks assist them in the initial public offering (IPO), when the company value (often estimated for the future potential more than the present earnings) is divided in a number of shares that are proposed to the investors on the stock market. By selling a fraction of their company, the original owners realize a capital gain, but also give up part of the control and future earnings to other shareholders. After a rapid and rather systematic evolution (depending on how well the investment bank succeeds in aligning the initial offering with the market expectations), the share price starts a dominantly random evolution in agreement with Fama's efficient market hypothesis introduced in section 1.4.

Previous experiments with the VMARKET applet suggested that possible realizations for the price of a share can be simulated by adding small increments to the initial price that is known. To be precise, the market (or spot) value can never be predicted with certainty, but an expected value can nevertheless be calculated, provided that the distribution of increments reproduces the market characteristics.

In addition to the deterministic growth (Drift parameter 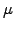$\mu$ ) and the random component associated with risk (Volatility parameter 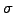$\sigma$ ), statistical analysis unveils a significant difference between the stock and the bond prices: the share price increments have a log-normal distribution, while the spot rate increments tend to have a more normal distribution. In other words, a share presently at EUR 10 is as likely to double in value to EUR 20 as it is to divide by two down to EUR 5. This in contrast with interest rates at 10%, which are as likely to rise (to 15%) or fall (to 5%) by the same amount. The VMARKET applet below illustrates the difference between the two distributions, assimilating the random horizontal motion of a red dot with the price of a share in a volatile market.

**VMARKET applet:** press **Start/Stop** and **Reset** to simulate possible evolutions of a spot price on the stock market using a log-normal distribution of daily price increments. The horizontal position of the red dot measures the value of the share and evolves as a function of time S(t), with small increments either to the left (when the price drops) or to the right (when it rises). Observe that the size of the increments is proportional to the spot price, with larger jumps on the right and smaller jumps on the left side of the window. Note that the left end corresponds to the limit where the share lost all of its value, i.e. the company is bankrupt!

Virtual market experiments: log-/normal price increments

Switch between a log-normal (LogNkappa=1) and a normal (LogNkappa=0) distribution of the increments and try to qualify the difference between the two evolutions.
Increase to Volatility=3 and Step 1 log-normal increment at a time. Take a few measurements showing that the jumps are often larger for high prices (to the right) than for low prices (to the left); they are on the contrary symmetric with a normal distribution.
Increase the Volatility further and check for both distributions if the price can ever become negative. Note that the numerical model produces wrong answers for large increments and large time steps; under realistic conditions, the volatility rarely approaches unity.

Masters: distribution of increments.
In the next chapter, we will study more carefully how the increment dS describing the random component of an asset price S is proportional to a the stochastic increment dX

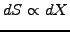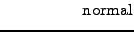$\displaystyle dS \propto dX$		$\displaystyle \hspace{2cm}\mathrm{normal}$	(2.1.1#eq.1)
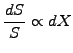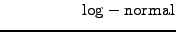$\displaystyle \frac{dS}{S} \propto dX$		$\displaystyle \hspace{2cm}\mathrm{log-normal}$	(2.1.1#eq.2)

where the increment dX can be evaluated as a random number drawn from a normal distribution with zero mean $\mathcal{N}[0,\sigma](x)$ (1.4#eq.5) to simulate relatively large time steps longer than one month. Very little programming experience is needed to understand how the log-normal walk (the position or the price) of a single particle has been implemented in VMARKET applet using the scheme

      double mu      = runData.getParamValue("Drift");
      double sigma   = runData.getParamValue("Volatility");

      for(int j=0; j<numberOfRealisations; j++){
        currentState[j][0] += currentState[j][0] * 
              ( mu*timeStep +
                random.nextGaussian()*sigma*Math.sqrt(timeStep) );
      }

For those who are not familiar with Java or C++ coding conventions, note that x+=1.0 increments the variable x by the real value one and j++ increments the variable j by the integer value one after using it for evaluation. Choosing the input parameter Drift=0.0 in the applet also sets mu=0.0, so that the normally distributed random number $\mathcal{N}[0,1]$ obtained from the function random.nextGaussian() is here simply scaled by the current position to simulate a log-normal distribution of the increments without drift.
For time steps shorter than one month, the random component of asset price increments is sometimes modeled with a Lévy stable symmetrical distribution

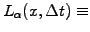$\displaystyle L_\alpha(x,\Delta t) \equiv$

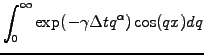$\displaystyle \int_0^\infty \exp(-\gamma\Delta t q^\alpha) \cos(qx) dq$

(2.1.1#eq.3)

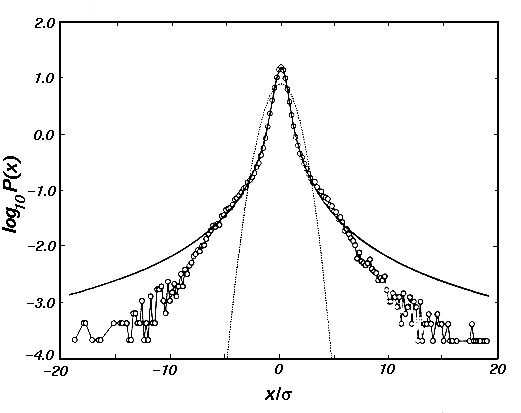
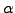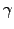The probability $P(0)\equiv L_\alpha(0,\Delta t) = \Gamma(1/\alpha)/(\pi\alpha\sqrt[\alpha]{\gamma\Delta t})$ with an index $\alpha$ =1.40 have been used in Ref.[15] to first calculate the scaling factor $\gamma$ =0.00375 and then reproduce nearly three orders of magnitude of the ``fat tails'' of a leptokurtotic distribution in (2.1.1#fig.1), here measured from spot price increments over time intervals as short as one minute.

Figure 2.1.1#fig.1: Distribution of the random variable dX observed to drive market price increments (circles) for a time interval as short as 1 min in a comparison with Lévy stable (solid line) and normal distributions (dots).
Market data, Normal & Lévy distributions of increments

At least some investors have to believe that the price of a share will rise more rapidly than the return they can earn overnight from a deposit at a spot rate, which carries little or no risk at all. A risk premium in the range 3-8% is usually added to the 0-2% spot rate to account for a positive drift proportional to the share value (e.g. Drift=SpotRate+0.04).

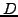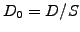A fixed dividend payment per share is often made each year after the shareholder's assembly; for simplicity, this can be modeled as a continuous dividend yield in the range 1-4% and contributes with a negative drift to the spot price, since the payments reduce the total value of the company (e.g. Drift=SpotRate-Dividend, see exercise 2.02).

**VMARKET applet:** press **Start/Stop** and **Reset** to simulate *Walkers=10000* possible evolutions starting from one single spot price of EUR 10, using a log-normal distribution of daily price increments. The black curve accumulates the number of realizations in a total of *MeshPoints=21* bins of unit width: it can be interpreted as the probability density of finding the spot price in a unit interval after a period of *Time* displayed on the top of the window. Click in the plot area to print the pointed coordinates (price [EUR], probability) onto the browser status bar and the browser console. Also, switch to *DistribFct* (without a star) and press *Toggle Display* twice to re-normalize log-normal distribution. After a quarter of year, you should measure approx 10% chances that the price lands in the interval [6.5;7.5]. Using a trapezoidal rule, quants can estimate the surface below the curve in the interval [0;10] and approximatively get 0.001+0.008+0.031+0.056+0.085+0.100+0.102+0.100+0.088+0.5*0.077=0.61: this corresponds to a probability of ~ 60% that the price drops after a quarter of a year. How is that possible?

Virtual market experiments: expectations

Assume reasonable values Drift=0.1, Volatility=0.5 and develop an intuition for what is a typical evolution of shares quoted on NASDAQ during RunTime=1.0 year. Measure the final price of a realization by clicking in the plot area and monitor the status field at the bottom of your browser.
Decrease the number of Walkers=100 and perform 2-3 simulations counting the number of prices that drop below the initial value. Quants compare with the area below the black line, which accumulates the realizations in MeshPoints-1=20 bins of unit length and should be interpreted as the probability density of reaching those prices. Explain your observations...
Switch to (DistribFct, without a star) and study the difference between the stock and bond markets using log-/normal distributions of the increments (LogNkappa=0 or 1); press Toggle Display to re-normalize.

Before we conclude this short introduction on the modeling of the prices on the stock market, simply note that any combination of shares can be used to form a weighted average called market index: the most famous such as the Dow Jones and NASDAQ 100 in the US, the FTSE 100 (Financial Times Stock Exchange, pronounce ``footsee'') in the UK and the Nikkei 225 in Japan combine the largest and most prestigious companies (so called ``blue chips'' - the name stems from the game of poker where the blue chip have the highest value) in a country and provide a measure of the economic growth of a nation.

SYLLABUS Previous: 2.1 The stock market Up: 2.1 The stock market Next: 2.1.2 Forward contract and