

 ','..','$myPermit') ?>
SYLLABUS Previous: 4.2 Exotic stock options
Up: 4.2 Exotic stock options
Next: 4.2.2 Barrier options
','..','$myPermit') ?>
SYLLABUS Previous: 4.2 Exotic stock options
Up: 4.2 Exotic stock options
Next: 4.2.2 Barrier options
4.2.1 Binary options
[ SLIDE
super-share -
cash-or-nothing ||
VIDEO
99) echo "
modem -
LAN -
DSL
"; else echo "login";?>
]
Binary or digital options are a straight forward extension of a plain
vanilla contract with a more general terminal payoff
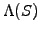 : as a
consequence, the solution methods and the payoff enjoy many of the same
features that have already been discussed for the put / call option.
The VMARKET applet below shows the
evolution of a super-share option for an increasing time to the expiry
date.
: as a
consequence, the solution methods and the payoff enjoy many of the same
features that have already been discussed for the put / call option.
The VMARKET applet below shows the
evolution of a super-share option for an increasing time to the expiry
date.
VMARKET applet: press Start/Stop
to study the payoff dynamics V(S,t) for a super-share option.
Change the SpotRate, Dividend and Volatility
parameters and review the dependencies previously discussed in the
case of vanilla instruments.
|
|
"; ?>
Apart from stretching the validity of the numerical method, the sharp
edges in the terminal payoff do seriously question whether it is
practically possible to perform the delta-hedging
in order to eliminate the uncertainty close to the expiry date.
Indeed, the option value jumps every time the underlying moves across
an edge, so that a large number of underlying shares have to be bought /
sold to keep the portfolio value deterministic. Transaction costs play
an increasingly important role and have to be taken into account
(exercise 3.05).
SYLLABUS Previous: 4.2 Exotic stock options
Up: 4.2 Exotic stock options
Next: 4.2.2 Barrier options


 ','..','$myPermit') ?>
SYLLABUS Previous: 4.2 Exotic stock options
Up: 4.2 Exotic stock options
Next: 4.2.2 Barrier options
','..','$myPermit') ?>
SYLLABUS Previous: 4.2 Exotic stock options
Up: 4.2 Exotic stock options
Next: 4.2.2 Barrier options
![]() : as a
consequence, the solution methods and the payoff enjoy many of the same
features that have already been discussed for the put / call option.
The VMARKET applet below shows the
evolution of a super-share option for an increasing time to the expiry
date.
: as a
consequence, the solution methods and the payoff enjoy many of the same
features that have already been discussed for the put / call option.
The VMARKET applet below shows the
evolution of a super-share option for an increasing time to the expiry
date.