

 SYLLABUS Previous: 2.3 Convertible bonds
Up: 2 A VARIETY OF
Next: 2.5 Computer quiz
SYLLABUS Previous: 2.3 Convertible bonds
Up: 2 A VARIETY OF
Next: 2.5 Computer quiz
2.4 Hedging parameters, portfolio sensitivity
[ SLIDE
delta -
gamma -
theta -
vega -
rho || same
VIDEO as previous section:
modem -
LAN -
DSL ]
The put-call parity in (2.1.3#eq.2) shows how a particular
combination of options with the underlying can be used to exactly
cancel the investment risk in a very simple situation.
The same trick could in principle be used for all the securities in
a portfolio
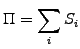 |
(2.4#eq.1) |
Such a hedging strategy is however neither practical nor does it in
general produce the desired effect: remember that, to achieve a certain
return, investors need to take a limited amount of risk - albeit in a
controlled manner that can be monitored to make sure that in the long
term the investment survives even large market fluctuations.
To quantify the sensitivity to small changes of a limited number of
parameters, the portfolio value is often expanded into a Taylor series
and the dominant terms labelled using Greek letters.
The largest contribution is usually delta and measures how the
value of the portfolio changes with the value of each individual asset
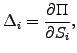 |
(2.4#eq.2) |
Gamma quantifies smaller effects due to the curvature
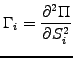 |
(2.4#eq.3) |
and vega (not a Greek letter) measures the sensitivity to changes in
the volatility
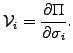 |
(2.4#eq.4) |
An extension including variation from any subset of the assets is
straightforward using gradients in multiple dimensions.
The so-called theta measures the decay of the value with time
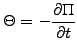 |
(2.4#eq.5) |
and rho the sensitivity to small variations in the interest rate
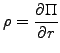 |
(2.4#eq.6) |
Finally, when a bond paying coupons Ai at times ti
is discounted to the present value B=å
Ai exp(-r ti) at a yield Y,
the duration measures how long on average the investor has to
wait before he recieves cash payments
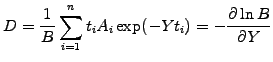 |
(2.4#eq.7) |
By monitoring and limiting the dependences to some of these factors,
hedgers can at least start to identify and reduce if not eliminate the
short term risk in a portfolio.
SYLLABUS Previous: 2.3 Convertible bonds
Up: 2 A VARIETY OF
Next: 2.5 Computer quiz


 SYLLABUS Previous: 2.3 Convertible bonds
Up: 2 A VARIETY OF
Next: 2.5 Computer quiz
SYLLABUS Previous: 2.3 Convertible bonds
Up: 2 A VARIETY OF
Next: 2.5 Computer quiz