

 ','..','$myPermit') ?>
SYLLABUS Previous: 2.1 The stock market
Up: 2.1 The stock market
Next: 2.1.2 Forward contract and
','..','$myPermit') ?>
SYLLABUS Previous: 2.1 The stock market
Up: 2.1 The stock market
Next: 2.1.2 Forward contract and
2.1.1 Shares and market indices
[ SLIDE
random walk -
log-normal -
Lévy -
drifts ||
VIDEO
99) echo "
modem -
LAN -
DSL
"; else echo "login";?>
]
Small companies generally start developing a product using private
resources and sometimes a limited amount of
venture capital. If all goes
well, they may under circumstance decide to go to the stock market
for the quest of new capital, which will allow them to grow more rapidly
than what they could achieve by simply re-investing their own earnings.
Investment banks
assist them in the initial public offering (IPO),
when the company value (often estimated for the future potential more than
the present earnings) is divided in a number of shares that are proposed
to the investors on the stock market. By selling a fraction of their
company, the original owners realize a
capital gain, but also give up part
of the control and future earnings to other shareholders. After a rapid
and rather systematic evolution (depending on how well the investment bank
succeeds in aligning the initial offering with the market expectations),
the share price starts a dominantly random evolution in agreement with
Fama's efficient market hypothesis
introduced in section 1.4.
Previous experiments with the VMARKET applet suggested that
possible realizations for the price of a share can be simulated by
adding small increments to the initial price that is known.
To be precise, the market (or spot)
value can never be predicted with certainty, but an
expected value
can nevertheless be calculated, provided that the distribution of
increments reproduces the market characteristics.
In addition to the deterministic growth (Drift parameter 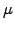 ) and the
random component associated with risk (Volatility parameter
) and the
random component associated with risk (Volatility parameter 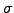 ),
statistical analysis unveils a significant difference between the stock and
the bond prices: the share price increments have a
log-normal distribution,
while the spot rate increments tend to have a more
normal distribution.
In other words, a share presently at EUR 10 is as likely to double in value
to EUR 20 as it is to divide by two down to EUR 5.
This in contrast with interest rates at 10%, which are as likely to rise
(to 15%) or fall (to 5%) by the same amount.
The VMARKET applet below illustrates the
difference between the two distributions, assimilating the random
horizontal motion of a red dot with the price of a share in a volatile
market.
),
statistical analysis unveils a significant difference between the stock and
the bond prices: the share price increments have a
log-normal distribution,
while the spot rate increments tend to have a more
normal distribution.
In other words, a share presently at EUR 10 is as likely to double in value
to EUR 20 as it is to divide by two down to EUR 5.
This in contrast with interest rates at 10%, which are as likely to rise
(to 15%) or fall (to 5%) by the same amount.
The VMARKET applet below illustrates the
difference between the two distributions, assimilating the random
horizontal motion of a red dot with the price of a share in a volatile
market.
VMARKET applet: press Start/Stop
and Reset to simulate possible evolutions of a spot price on the
stock market using a log-normal distribution of daily price increments.
The horizontal position of the red dot measures the value of the share
and evolves as a function of time S(t), with small increments either to
the left (when the price drops) or to the right (when it rises).
Observe that the size of the increments is proportional to the spot
price, with larger jumps on the right and smaller jumps on the left
side of the window.
Note that the left end corresponds to the limit where the share lost
all of its value, i.e. the company is bankrupt!
|
|
"; ?>
";?>
Masters: distribution of increments.
In the next chapter, we will study more carefully how the increment dS
describing the random component of an asset price S is proportional to
a the stochastic increment dX
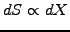 |
|
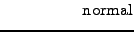 |
(2.1.1#eq.1) |
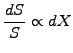 |
|
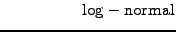 |
(2.1.1#eq.2) |
";?>
where the increment dX can be evaluated as a random number drawn from a
normal distribution
with zero mean
$](s2img48.gif) (1.4#eq.5) to simulate
relatively large time steps longer than one month.
Very little programming experience is needed to understand how the
log-normal walk (the position or the price) of a single particle has
been
implemented in VMARKET
applet using the scheme
(1.4#eq.5) to simulate
relatively large time steps longer than one month.
Very little programming experience is needed to understand how the
log-normal walk (the position or the price) of a single particle has
been
implemented in VMARKET
applet using the scheme
double mu = runData.getParamValue("Drift");
double sigma = runData.getParamValue("Volatility");
for(int j=0; j<numberOfRealisations; j++){
currentState[j][0] += currentState[j][0] *
( mu*timeStep +
random.nextGaussian()*sigma*Math.sqrt(timeStep) );
}
For those who are not familiar with Java or C++ coding conventions, note
that x+=1.0 increments the variable x by the real value one
and j++ increments the variable j by the integer value one after
using it for evaluation.
Choosing the input parameter Drift=0.0 in the applet also sets
mu=0.0, so that the normally distributed random number
![$ \mathcal{N}[0,1]$](s2img49.gif) obtained from the function
obtained from the function random.nextGaussian()
is here simply scaled by the current position to simulate a log-normal
distribution of the increments without drift.
For time steps shorter than one month, the random component of asset price
increments is sometimes modeled with a Lévy stable symmetrical distribution
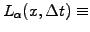 |
|
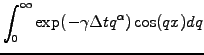 |
(2.1.1#eq.3) |
";?>
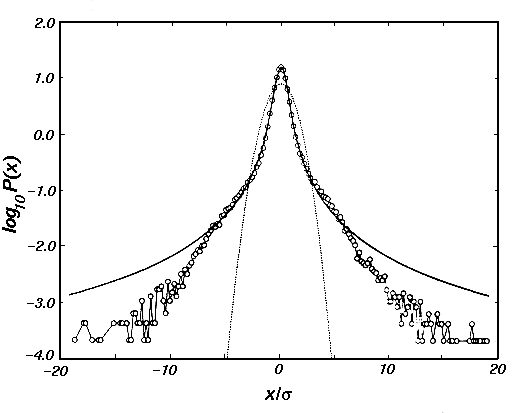
The probability
![$ P(0)\equiv L_\alpha(0,\Delta t) =
\Gamma(1/\alpha)/(\pi\alpha\sqrt[\alpha]{\gamma\Delta t})$](s2img52.gif) with an index
with an index 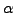 =1.40 have been used in Ref.[15] to first
calculate the scaling factor
=1.40 have been used in Ref.[15] to first
calculate the scaling factor 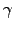 =0.00375 and then reproduce nearly
three orders of magnitude of the ``fat tails'' of a leptokurtotic
distribution in (2.1.1#fig.1), here measured from spot price increments
over time intervals as short as one minute.
=0.00375 and then reproduce nearly
three orders of magnitude of the ``fat tails'' of a leptokurtotic
distribution in (2.1.1#fig.1), here measured from spot price increments
over time intervals as short as one minute.
Figure 2.1.1#fig.1:
Distribution of the random variable dX observed to drive market price
increments (circles) for a time interval as short as 1 min in a comparison
with Lévy stable (solid line) and normal distributions (dots).
|
At least some investors have to believe that the price of a share will
rise more rapidly than the return they can earn overnight from a deposit
at a spot rate, which carries little or no risk at all.
A risk premium in the range 3-8% is
usually added to the 0-2% spot rate to account for a positive drift
proportional to the share value (e.g. Drift=SpotRate+0.04).
A fixed dividend payment 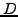 per share is often made each year after
the shareholder's assembly; for simplicity, this can be modeled as a
continuous dividend yield
per share is often made each year after
the shareholder's assembly; for simplicity, this can be modeled as a
continuous dividend yield 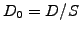 in the range 1-4% and contributes
with a negative drift to the spot price, since the payments reduce
the total value of the company (e.g. Drift=SpotRate-Dividend,
see exercise 2.02).
in the range 1-4% and contributes
with a negative drift to the spot price, since the payments reduce
the total value of the company (e.g. Drift=SpotRate-Dividend,
see exercise 2.02).
VMARKET applet: press Start/Stop
and Reset to simulate Walkers=10000 possible evolutions
starting from one single spot price of EUR 10, using a log-normal
distribution of daily price increments.
The black curve accumulates the number of realizations in a total of
MeshPoints=21 bins of unit width: it can be interpreted as the
probability density of finding the spot price in a unit interval after
a period of Time displayed on the top of the window.
Click in the plot area to print the pointed coordinates (price [EUR],
probability) onto the browser status bar and the browser console.
Also, switch to DistribFct (without a star) and press
Toggle Display twice to re-normalize log-normal distribution.
After a quarter of year, you should measure approx 10% chances that
the price lands in the interval [6.5;7.5].
Using a trapezoidal rule, quants can estimate the surface below the
curve in the interval [0;10] and approximatively get
0.001+0.008+0.031+0.056+0.085+0.100+0.102+0.100+0.088+0.5*0.077=0.61:
this corresponds to a probability of ~ 60% that the price drops after
a quarter of a year. How is that possible?
|
|
"; ?>
Before we conclude this short introduction on the modeling of the prices on
the stock market, simply note that any combination of shares can be used to
form a weighted average called market index: the most famous such as the
Dow Jones
and
NASDAQ 100
in the US,
the FTSE 100
(Financial Times Stock Exchange, pronounce ``footsee'') in the UK and the
Nikkei 225
in
Japan combine the largest and most prestigious companies (so called ``blue
chips'' - the name stems from the game of poker where the blue chip have
the highest value) in a country and provide a measure of the economic growth
of a nation.
SYLLABUS Previous: 2.1 The stock market
Up: 2.1 The stock market
Next: 2.1.2 Forward contract and


 ','..','$myPermit') ?>
SYLLABUS Previous: 2.1 The stock market
Up: 2.1 The stock market
Next: 2.1.2 Forward contract and
','..','$myPermit') ?>
SYLLABUS Previous: 2.1 The stock market
Up: 2.1 The stock market
Next: 2.1.2 Forward contract and
![]() ) and the
random component associated with risk (Volatility parameter
) and the
random component associated with risk (Volatility parameter ![]() ),
statistical analysis unveils a significant difference between the stock and
the bond prices: the share price increments have a
log-normal distribution,
while the spot rate increments tend to have a more
normal distribution.
In other words, a share presently at EUR 10 is as likely to double in value
to EUR 20 as it is to divide by two down to EUR 5.
This in contrast with interest rates at 10%, which are as likely to rise
(to 15%) or fall (to 5%) by the same amount.
The VMARKET applet below illustrates the
difference between the two distributions, assimilating the random
horizontal motion of a red dot with the price of a share in a volatile
market.
),
statistical analysis unveils a significant difference between the stock and
the bond prices: the share price increments have a
log-normal distribution,
while the spot rate increments tend to have a more
normal distribution.
In other words, a share presently at EUR 10 is as likely to double in value
to EUR 20 as it is to divide by two down to EUR 5.
This in contrast with interest rates at 10%, which are as likely to rise
(to 15%) or fall (to 5%) by the same amount.
The VMARKET applet below illustrates the
difference between the two distributions, assimilating the random
horizontal motion of a red dot with the price of a share in a volatile
market.
![]() per share is often made each year after
the shareholder's assembly; for simplicity, this can be modeled as a
continuous dividend yield
per share is often made each year after
the shareholder's assembly; for simplicity, this can be modeled as a
continuous dividend yield ![]() in the range 1-4% and contributes
with a negative drift to the spot price, since the payments reduce
the total value of the company (e.g. Drift=SpotRate-Dividend,
see exercise 2.02).
in the range 1-4% and contributes
with a negative drift to the spot price, since the payments reduce
the total value of the company (e.g. Drift=SpotRate-Dividend,
see exercise 2.02).