

 SYLLABUS Previous: 3.3.3 Evaluate an expectancy
Up: 3 FORECASTING WITH UNCERTAINTY
Next: 3.5 Hedging a bond
SYLLABUS Previous: 3.3.3 Evaluate an expectancy
Up: 3 FORECASTING WITH UNCERTAINTY
Next: 3.5 Hedging a bond
3.4 Hedging an option with the underlying (Black-Scholes)
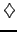
[ SLIDE
portfolio -
no random -
no arbitrage -
Black-Scholes -
properties ||
VIDEO
modem -
LAN -
DSL]
Take a log-normal distribution of the price increments 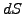 in (3.3.1#eq.1)
modeling the price evolution of a share
in (3.3.1#eq.1)
modeling the price evolution of a share 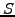 with a volatility
with a volatility 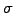 in
an efficient market where all the risk-free portfolios earn the same
deterministic spot rate
in
an efficient market where all the risk-free portfolios earn the same
deterministic spot rate 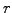 .
For simplicity, neglect the payment of dividends
.
For simplicity, neglect the payment of dividends 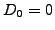 and assume
that the underlying trades continuously without transaction costs
and assume
that the underlying trades continuously without transaction costs  (extensions are considered in exercises 3.03 & 3.04).
(extensions are considered in exercises 3.03 & 3.04).
Now construct a portfolio combining an option (or indeed any kind of
stock market derivative) with a value 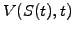 and an unspecified,
but constant number
and an unspecified,
but constant number 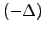 of the underlying share. The initial
value of this portfolio and its incremental change per time-step are
of the underlying share. The initial
value of this portfolio and its incremental change per time-step are
 |
(3.4#eq.1) |
Using Itô's lemma (3.3.2#eq.2) to substitute for the stochastic
value of the option price increment 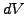 and choosing
and choosing 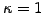 for a log-normal walk with (3.3.1#eq.1), this yields
for a log-normal walk with (3.3.1#eq.1), this yields
![$\displaystyle d\Pi=\left[\frac{\partial V}{\partial t} +\mu S \frac{\partial V}...
...ta \right] dt +\sigma S \left[\frac{\partial V}{\partial S}-\Delta\right] dW(t)$](s3img124.gif) |
(3.4#eq.2) |
The random term in 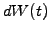 can now be eliminated by continuously hedging
the portfolio so as to maintain the number of shares equal to
can now be eliminated by continuously hedging
the portfolio so as to maintain the number of shares equal to
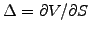 .
With this choice, the portfolio becomes deterministic (risk-free) and,
using the standard no-arbitrage arguments,
must earn the same amount as the risk-free return
.
With this choice, the portfolio becomes deterministic (risk-free) and,
using the standard no-arbitrage arguments,
must earn the same amount as the risk-free return 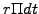 payed when
an amount of cash
payed when
an amount of cash  is invested at a spot rate
is invested at a spot rate  during a small
time
during a small
time 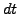 . Equating both earnings
. Equating both earnings
![$\displaystyle d\Pi=\left[ \frac{\partial V}{\partial t} +\frac{1}{2}\sigma^2 S^2\frac{\partial^2 V}{\partial S^2}\right] dt = r\Pi dt$](s3img128.gif) |
(3.4#eq.3) |
leads directly to the celebrated Black-Scholes equation [3]
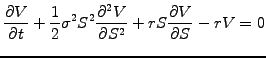 |
(3.4#eq.4) |
which shows that the return of a delta-hedged portfolio (first two term)
is exactly balanced by the return on a bank deposit (last two terms).
The equation describes the price of stock options (call, put and indeed
any derivative security where the price 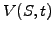 depends only on the
spot price and time) in a market that is parametrized by the volatility
depends only on the
spot price and time) in a market that is parametrized by the volatility
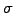 and the spot rate
and the spot rate 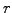 .
An important finding is that the price of an option does not explicitly
depend on how rapidly the underlying asset grows: the drift
.
An important finding is that the price of an option does not explicitly
depend on how rapidly the underlying asset grows: the drift 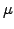 does not explicitly appear in the Black-Scholes equation. The reason
is that the option price has been calculated relative to the underlying,
so that the drift is here already accounted for in an implicit manner.
does not explicitly appear in the Black-Scholes equation. The reason
is that the option price has been calculated relative to the underlying,
so that the drift is here already accounted for in an implicit manner.
In mathematics (3.4#eq.4) is known as a
partial differential equation
(since it has partial derivatives up to first order in time
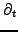 and second order in the asset price
and second order in the asset price
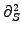 ) of backward parabolic type
(backward because both these derivatives have the same sign,
parabolic since this combination of coefficients yields exactly one
characteristic).
In physics, it bears a strong resemblance with the heat equation, except
that here it is the price of an option that is diffusing with respect to
the underlying rather than heat diffusing in space.
) of backward parabolic type
(backward because both these derivatives have the same sign,
parabolic since this combination of coefficients yields exactly one
characteristic).
In physics, it bears a strong resemblance with the heat equation, except
that here it is the price of an option that is diffusing with respect to
the underlying rather than heat diffusing in space.
To solve the Black-Scholes equation backward in time, a final
condition needs to be imposed at expiry 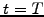 reproducing the
terminal payoff
reproducing the
terminal payoff
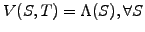 discussed in
chapter 2.
Boundary conditions have to be imposed on the price boundaries
and are obtained from additional no-arbitrage arguments.
A vanilla put option, for example, is increasingly unlikely to be
exercised when the price of the underlying gets very large, so that
the value of a put
discussed in
chapter 2.
Boundary conditions have to be imposed on the price boundaries
and are obtained from additional no-arbitrage arguments.
A vanilla put option, for example, is increasingly unlikely to be
exercised when the price of the underlying gets very large, so that
the value of a put
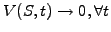 when
when
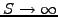 .
On the lower boundary, (3.3.1#eq.1) shows that the log-normal price
increments of the underlying vanish
.
On the lower boundary, (3.3.1#eq.1) shows that the log-normal price
increments of the underlying vanish
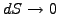 when
when
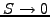 , so that the problem becomes deterministic: a put option
that is certain to be exercised for a price
, so that the problem becomes deterministic: a put option
that is certain to be exercised for a price 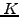 at the expiry can be
discounted back to the present value
at the expiry can be
discounted back to the present value
![$ V(0,t)=K\exp[-r(T-t)]$](s3img139.gif) .
Similar arguments will be used to derive the conditions for a call option
in section 4.4.
.
Similar arguments will be used to derive the conditions for a call option
in section 4.4.
SYLLABUS Previous: 3.3.3 Evaluate an expectancy
Up: 3 FORECASTING WITH UNCERTAINTY
Next: 3.5 Hedging a bond


 SYLLABUS Previous: 3.3.3 Evaluate an expectancy
Up: 3 FORECASTING WITH UNCERTAINTY
Next: 3.5 Hedging a bond
SYLLABUS Previous: 3.3.3 Evaluate an expectancy
Up: 3 FORECASTING WITH UNCERTAINTY
Next: 3.5 Hedging a bond