

 ','..','$myPermit') ?>
SYLLABUS Previous: 1.2 Differential Equations
Up: 1.2 Differential Equations
Next: 1.2.2 Partial differential equations
','..','$myPermit') ?>
SYLLABUS Previous: 1.2 Differential Equations
Up: 1.2 Differential Equations
Next: 1.2.2 Partial differential equations
1.2.1 Ordinary differential equations
Slide : [ ODE
Euler -
mid-point rule -
Runge-Kutta ||
VIDEO
99) echo "
modem -
ISDN -
LAN
"; else echo "login";?>
]
Rather than repeating details of elementary numerical analysis, this section
is only meant to review a few methods that will be used later, e.g. in the
chapter dealing with the Monte Carlo method for partial differential equations
(PDE).
Ordinary differential equations (ODE) are often encountered when dealing with
initial value problems. In Newtonian mechanics, for example, the trajectory
of a particle is described by an evolution in time
The example shows how higher order equations can be recast into a system
of first order equations, with components of the form
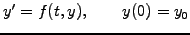 |
(1.2.1#eq.1) |
Under very general assumptions, an initial condition 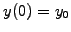 having
the same number of components as the unknown vector
having
the same number of components as the unknown vector 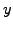 yields exactly
one solution to (1.2.1#eq.1), which can then be approximated with a
computer.
yields exactly
one solution to (1.2.1#eq.1), which can then be approximated with a
computer.
Introducing a discretization
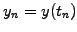 with a finite number
with a finite number 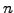 of
time steps
of
time steps
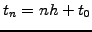 , a straight forward manner to solve an ODE is
to approximate the derivative with a finite difference quotient forward
in time
, a straight forward manner to solve an ODE is
to approximate the derivative with a finite difference quotient forward
in time
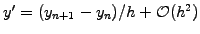 , leading to the
Euler recursion formula
, leading to the
Euler recursion formula
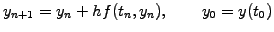 |
(1.2.1#eq.2) |
Because all the quantities are known at time 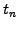 , the scheme is said
to be explicit. An implicit evaluation of the function
, the scheme is said
to be explicit. An implicit evaluation of the function
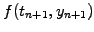 is sometimes desirable in order to stabilize the
propagation of numerical errors; this is however computationally
expensive when the function cannot be inverted analytically.
is sometimes desirable in order to stabilize the
propagation of numerical errors; this is however computationally
expensive when the function cannot be inverted analytically.
More precision can be obtained by using a finite difference quotient
symmetric in time
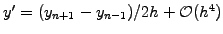 ,
which is obtained by summing two Taylor series forward and backward
(exercise 1.02). This yields the so-called midpoint formula
,
which is obtained by summing two Taylor series forward and backward
(exercise 1.02). This yields the so-called midpoint formula
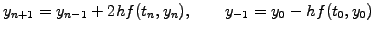 |
(1.2.1#eq.3) |
which is second order accurate, but requires a special initialization
to generate the additional values that are needed from the past. Writing
the mid-point rule as
the initialization problem is cured and leads to the famous
second order Runge-Kutta method
Such elementary and more sophisticated methods are commonly available
in software packages such as OCTAVE and MATLAB; type
help ode23 to find out more about how to use them.
Methods for ordinary equations are usually robust; however, they become
extremely inefficient when a problem is stiff, i.e. involves two
very different scales by limiting the step size to the shorter scale
even when this is not at all relevant (exercise 1.06).
SYLLABUS Previous: 1.2 Differential Equations
Up: 1.2 Differential Equations
Next: 1.2.2 Partial differential equations
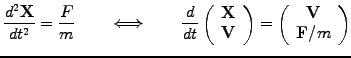


 ','..','$myPermit') ?>
SYLLABUS Previous: 1.2 Differential Equations
Up: 1.2 Differential Equations
Next: 1.2.2 Partial differential equations
','..','$myPermit') ?>
SYLLABUS Previous: 1.2 Differential Equations
Up: 1.2 Differential Equations
Next: 1.2.2 Partial differential equations
![]() with a finite number
with a finite number ![]() of
time steps
of
time steps
![]() , a straight forward manner to solve an ODE is
to approximate the derivative with a finite difference quotient forward
in time
, a straight forward manner to solve an ODE is
to approximate the derivative with a finite difference quotient forward
in time
![]() , leading to the
Euler recursion formula
, leading to the
Euler recursion formula
![]() ,
which is obtained by summing two Taylor series forward and backward
(exercise 1.02). This yields the so-called midpoint formula
,
which is obtained by summing two Taylor series forward and backward
(exercise 1.02). This yields the so-called midpoint formula