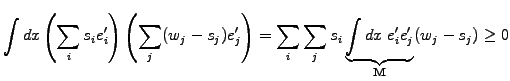','..','$myPermit') ?>
SYLLABUS Previous: 3.5 Linear solvers
Up: 3 FINITE ELEMENT METHOD
Next: 3.7 Computer quiz
','..','$myPermit') ?>
SYLLABUS Previous: 3.5 Linear solvers
Up: 3 FINITE ELEMENT METHOD
Next: 3.7 Computer quiz
3.6 Variational inequalities
Slide : [
obstacle problem -
complementarity form -
variational form ||
VIDEO
99) echo "
modem -
ISDN -
LAN
"; else echo "login";?>
]
Consider the simplest obstacle problem, which arises when an
elastic string held fixed at both ends is pulled over a smooth object
and an equilibrium is sought without knowing a priori where are the
regions of contact between the string and this object.
Define the function
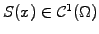 measuring the
elevation of the string in the interval
measuring the
elevation of the string in the interval
![$ \Omega=[x_L;x_R]$](s3img153.gif) and the
function
and the
function
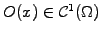 modeling the shape of the
object.
modeling the shape of the
object.
Mathematically, the obstacle problem amounts to finding a solution
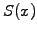 satisfying the conditions:
satisfying the conditions:
- the string always remains above the obstacle
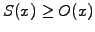 ,
,
- the string satisfies the equilibrium equation. Neglecting the
inertia, this says that the string has either zero curvature
(straight line between the points of contact) or a negative curvature
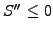 (line of contact - in other words, the
obstacle can only push the string up, not pull it down).
(line of contact - in other words, the
obstacle can only push the string up, not pull it down).
This section considers two methods for solving problems that involve
inequalities.
 Linear complementary formulation.
Linear complementary formulation.
- Reassemble all the constraints in a form
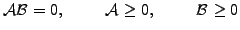 |
(1) |
After discretization, assuming
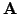 invertible and positive
definite, the linear problem
invertible and positive
definite, the linear problem
 |
(2) |
can be solved with the so-called projected SOR method, by replacing
(3.5#eq.10) with
![$\displaystyle \mathbf{x_{k+1}} = \max[\mathbf{c}, \omega \mathbf{x_{k}^{GS}} +(1-\omega) \mathbf{x_{k}} ]$](s3img160.gif) |
(3) |
and making sure that the iteration starts from an initial guess
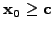 .
.
For the obstacle problem, the string follows either a straight line
above the obstacle
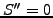 or fits exactly the object
or fits exactly the object
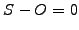 ; this leads to a complementary problem
; this leads to a complementary problem
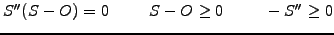 |
(4) |
which be discretized using finite differences and solved with the
projected SOR method (exercise 3.05).
 Variational formulation.
Variational formulation.
- This approach is particularly well suited for a discretization with
finite elements is and best illustrated directly with the example.
Choose a test function
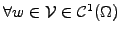 that satisfies the same constraints as the solution
that satisfies the same constraints as the solution
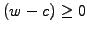 .
Having already
.
Having already
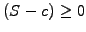 and
and
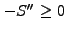 , write two
inequalities
, write two
inequalities
and subtract them
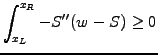 |
(5) |
The constraint 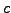 now appears only implicitly through the fact that
now appears only implicitly through the fact that
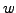 and
and 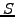 are members of the same sub-space
are members of the same sub-space
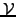 ; all what
remains to be done is to prove that the inequality (3.6#eq.5)
in fact is a strict equality if the solution satisfies the constraint.
After integration by parts and discretization with linear FEMs, the
problem can therefore be solved with projected SOR iterations
(3.6#eq.3, exercises 3.05 and 3.07).
; all what
remains to be done is to prove that the inequality (3.6#eq.5)
in fact is a strict equality if the solution satisfies the constraint.
After integration by parts and discretization with linear FEMs, the
problem can therefore be solved with projected SOR iterations
(3.6#eq.3, exercises 3.05 and 3.07).
To prove that (3.6#eq.5) satisfies a strict equality, integrate by
part and a discretize
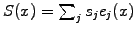 and
and
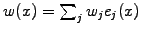 with linear finite elements
with linear finite elements
If the matrix is symmetric
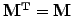 as is the case with
diffusion, this simply yields
as is the case with
diffusion, this simply yields
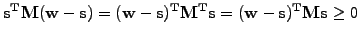 |
(6) |
If the problem is positive definite
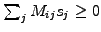 as is the case
with diffusion and the solution satisfies the constraint
as is the case
with diffusion and the solution satisfies the constraint
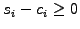 ,
the product satisfies the inequality
,
the product satisfies the inequality
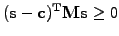 |
(7) |
Since (3.6#eq.6) must hold for the particular choice where the
test function coincides with the constraint
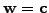 ,
the last two inequalities can only be satisfied simultaneously if
they both satisfy the strict equality.
,
the last two inequalities can only be satisfied simultaneously if
they both satisfy the strict equality.
SYLLABUS Previous: 3.5 Linear solvers
Up: 3 FINITE ELEMENT METHOD
Next: 3.7 Computer quiz


 ','..','$myPermit') ?>
SYLLABUS Previous: 3.5 Linear solvers
Up: 3 FINITE ELEMENT METHOD
Next: 3.7 Computer quiz
','..','$myPermit') ?>
SYLLABUS Previous: 3.5 Linear solvers
Up: 3 FINITE ELEMENT METHOD
Next: 3.7 Computer quiz
![]() measuring the
elevation of the string in the interval
measuring the
elevation of the string in the interval
![]() and the
function
and the
function
![]() modeling the shape of the
object.
modeling the shape of the
object.
![]() satisfying the conditions:
satisfying the conditions:
![]() or fits exactly the object
or fits exactly the object
![]() ; this leads to a complementary problem
; this leads to a complementary problem
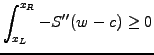
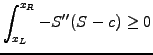
![]() and
and
![]() with linear finite elements
with linear finite elements