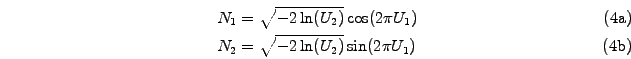','..','$myPermit') ?>
SYLLABUS Previous: 5.3 Particle orbits
Up: 5 MONTE-CARLO METHOD
Next: 5.5 When should you
','..','$myPermit') ?>
SYLLABUS Previous: 5.3 Particle orbits
Up: 5 MONTE-CARLO METHOD
Next: 5.5 When should you
5.4 A scheme for the advection diffusion equation
Slide : [
scheme -
Box-Mueller ||
VIDEO
99) echo "
modem -
ISDN -
LAN
"; else echo "login";?>
]
Let us use now the Feynman-Kac theorem and evolve a large number of
stochastic particle orbits to approximate the advection diffusion equation
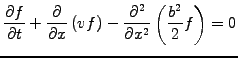 |
(1) |
The rules of the Itô calculus require the time discretization to be explicit
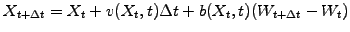 |
(2) |
Note that it is in fact possible to construct implicit discretizations of a
stochastic differential equation [22], but the construction it not
as simple as it is for ordinary equations (5.3#eq.3).
Since
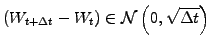 ,
the Wiener process can be written explicitly
,
the Wiener process can be written explicitly
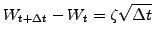 |
(3) |
where
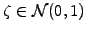 are normally distributed random numbers.
The central limit theorem states that any large sum involving
are normally distributed random numbers.
The central limit theorem states that any large sum involving 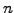 random
numbers equally distributed with zero mean and unit variance will eventually
converge to
random
numbers equally distributed with zero mean and unit variance will eventually
converge to
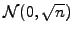 .
Any such random number could therefore be used for
.
Any such random number could therefore be used for 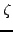 provided that
the number of time steps used to approximate the differential is large enough;
choosing
provided that
the number of time steps used to approximate the differential is large enough;
choosing
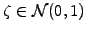 however leads to the fastest convergence.
however leads to the fastest convergence.
A numerical Monte Carlo scheme for the advection-diffusion equation is now
constructed, using 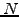 particles to sample the possible outcomes of the
entire ensemble of orbits
particles to sample the possible outcomes of the
entire ensemble of orbits
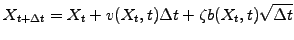 |
(4) |
This is simply be
implemented as
for(int j = 0; j < numberOfParticles; j++){
particlePosition[j] += velocity * timeStep +
random.nextGaussian() *
Math.sqrt(2 * diffusCo * timeStep);
// Insert here your periodic boundary conditions (exercise 5.03)
}
and can be tested in the JBONE applet below
JBONE applet: press Start/Stop
to solve the advection-diffusion equation with 1000 random walkers
initialized so as to approximate a box function.
Switch to Particle methods* to display the position of each
particle (red dots) in addition to the density distribution (black
line) obtained from a linear assignment of the position on a grid.
|
|
"; ?>
JAVA is one of the few programming languages that has a normal
pseudo random numbers generator
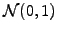 .
Other programming languages generally provide only uniform pseudo random
numbers
.
Other programming languages generally provide only uniform pseudo random
numbers
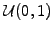 and the Box Müller method can then be
used to transfrom them into
and the Box Müller method can then be
used to transfrom them into
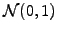 with the algorithm:
with the algorithm:
- Construct two uniformly distributed random numbers
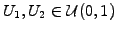 .
.
- Then
are two independent pseudo random numbers in
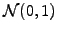 .
.
The rest of the implementation is equivalent if one remembers the
definition of the command x+=dx as being equivalent to
x=x+dx.
SYLLABUS Previous: 5.3 Particle orbits
Up: 5 MONTE-CARLO METHOD
Next: 5.5 When should you
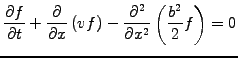


 ','..','$myPermit') ?>
SYLLABUS Previous: 5.3 Particle orbits
Up: 5 MONTE-CARLO METHOD
Next: 5.5 When should you
','..','$myPermit') ?>
SYLLABUS Previous: 5.3 Particle orbits
Up: 5 MONTE-CARLO METHOD
Next: 5.5 When should you
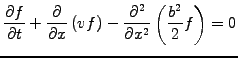
![]() particles to sample the possible outcomes of the
entire ensemble of orbits
particles to sample the possible outcomes of the
entire ensemble of orbits
![]() .
Other programming languages generally provide only uniform pseudo random
numbers
.
Other programming languages generally provide only uniform pseudo random
numbers
![]() and the Box Müller method can then be
used to transfrom them into
and the Box Müller method can then be
used to transfrom them into
![]() with the algorithm:
with the algorithm: