

 ','..','$myPermit') ?>
SYLLABUS Previous: 7 WAVELETS
Up: 7 WAVELETS
Next: JBONE user manual
','..','$myPermit') ?>
SYLLABUS Previous: 7 WAVELETS
Up: 7 WAVELETS
Next: JBONE user manual
7.1 Remain a matter of research
Slide : [
Links
]
There is a growing interest in using wavelets not only for the
discretization of functions (sect.1.4), but also to approximate
differential and integral operators.
Motivations for that are the potential gain of solving global problems
with the same number
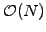 of operations as there are unknowns,
relying on recent advances in iterative methods (sect.3.5) to solve
linear systems in sparse format.
Having not had the possibility so far to implement wavelets into the
JBONE applet and extract the essence of research papers in a
pedagogical manner, this section is still limited to a number of links
to papers maintained on a web site from
MathSoft:
of operations as there are unknowns,
relying on recent advances in iterative methods (sect.3.5) to solve
linear systems in sparse format.
Having not had the possibility so far to implement wavelets into the
JBONE applet and extract the essence of research papers in a
pedagogical manner, this section is still limited to a number of links
to papers maintained on a web site from
MathSoft:
- D. M. Bond and S. A. Vavasis,
Fast Wavelet Transforms for Matrices Arising From Boundary Element Methods.
- T. Chan, W. Tang and W. Wan,
Wavelet sparse approximate inverse preconditioners
- P. Charton and V. Perrier,
Factorisation sur Bases d'Ondelettes du Noyeau de la Chaleur et
Algorithmes Matriciels Rapides Associes
- P. Charton and V. Perrier,
Towards a Wavelet Based Numerical Scheme for the Two-Dimensional
Navier-Stokes Equations.
- P. Charton and V. Perrier,
A Pseudo-Wavelet Scheme for the Two-Dimensional Navier-Stokes Equations.
- S. Dahlke and A. Kunoth,
Biorthogonal Wavelets and Multigrid.
- S. Dahlke and I. Weinreich,
Wavelet-Galerkin Methods: An Adapted Biorthogonal Wavelet Basis.
- S. Dahlke and I. Weinreich,
Wavelet Bases Adapted to Pseudo-Differential Operators.
- W. Dahmen and A. Kunoth,
Multilevel Preconditioning.
- R. Glowinski, T. Pan , R. O. Wells, Jr. and X. Zhou,
Wavelet and Finite Element Solutions for the Neumann Problem
Using Fictitious Domains
- R. Glowinski, A. Rieder, R. O. Wells, Jr. and X. Zhou,
A Wavelet Multigrid Preconditioner for Dirichlet Boundary Value
Problems in General Domains.
- R. Glowinski, A. Rieder, R. O. Wells, Jr. and X. Zhou,
A Preconditioned CG-Method for Wavelet-Galerkin Discretizations of
Elliptic Problems
- F. Heurtaux, F. Planchon and M. V. Wickerhauser,
Scale Decomposition in Burgers' Equation
- A. Jiang,
Fast wavelet based methods for certain time dependent problems
- A. Kunoth,
Multilevel Preconditioning - Appending Boundary Conditions by
Lagrange Multipliers.
- J. Lewalle,
Wavelet Transforms of some Equations of Fluid Mechanics
- J. Lewalle,
Energy Dissipation in the Wavelet-Transformed Navier-Stokes Equations
- J. Lewalle,
On the effect of boundary conditions on the multifractal statistics of
incompressible turbulence
- J. Lewalle,
Diffusion is Hamiltonian
- D. Lu, T. Ohyoshi and L. Zhu,
Treatment of Boundary Conditions in the Application of Wavelet-Galerkin
Method to a SH Wave Problem
- A. Rieder and X. Zhou,
On the Robustness of the Damped V-Cycle of the Wavelet Frequency
Decompositions Multigrid Method
- A. Rieder, R. O. Wells, Jr. and X. Zhou,
A Wavelet Approach to Robust Multilevel Solvers for Anisotropic Elliptic
Problems.
- A. Rieder, R. O. Wells, Jr. and X. Zhou,
On the Wavelet Frequency Decomposition Method
- O. V. Vasilyev and S. Paolucci,
A Dynamically Adaptive Multilevel Wavelet Collocation Method for Solving
Partial Differential Equations in a Finite Domain.
- O. V. Vasilyev, S. Paolucci and M. Sen,
A Multilevel Wavelet Collocation Method for Solving Partial
Differential Equations in a Finite Domain.
- R. O. Wells, Jr. and X. Zhou,
Wavelet Solutions for the Dirichlet Problem
- R. O. Wells, Jr. and X. Zhou,
Wavelet Interpolation and Approximate Solution of Elliptic Partial
Differential Equations
- R. O. Wells, Jr. and X. Zhou,
Representing the Geometry of Domains by Wavelets with Applications to
Partial Differential Equations
- R. O. Wells, Jr.,
Multiscale Applications of Wavelets to Solutions f Partial Differential
Equations
SYLLABUS Previous: 7 WAVELETS
Up: 7 WAVELETS
Next: JBONE user manual


 ','..','$myPermit') ?>
SYLLABUS Previous: 7 WAVELETS
Up: 7 WAVELETS
Next: JBONE user manual
','..','$myPermit') ?>
SYLLABUS Previous: 7 WAVELETS
Up: 7 WAVELETS
Next: JBONE user manual
![]() of operations as there are unknowns,
relying on recent advances in iterative methods (sect.3.5) to solve
linear systems in sparse format.
Having not had the possibility so far to implement wavelets into the
JBONE applet and extract the essence of research papers in a
pedagogical manner, this section is still limited to a number of links
to papers maintained on a web site from
MathSoft:
of operations as there are unknowns,
relying on recent advances in iterative methods (sect.3.5) to solve
linear systems in sparse format.
Having not had the possibility so far to implement wavelets into the
JBONE applet and extract the essence of research papers in a
pedagogical manner, this section is still limited to a number of links
to papers maintained on a web site from
MathSoft: