

 SYLLABUS Previous: 2.2.3 Interest rate swaps
Up: 2.2 The credit market
Next: 2.3 Convertible bonds
SYLLABUS Previous: 2.2.3 Interest rate swaps
Up: 2.2 The credit market
Next: 2.3 Convertible bonds
2.2.4 Bond options: caps, floors and swaptions
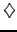
[ SLIDE
bond option -
cap/floor -
swaption ||
VIDEO
modem -
LAN -
DSL]
In the same manner as stock market derivatives have been introduced in
section 2.1.3 for an underlying share, different types of
credit market derivatives confer the holder a right to buy or sell the
earnings from interest rates.
The simplest is the bond option, which confers its holder the right
to buy or sell an underlying discount bond with a maturity TB
that is necessarily longer than the option expiry T<TB.
Using the notation VB(r,t,TB)
for the value of the discount bond before the maturity (something that
we will calculate later in chapter 5) the terminal conditions
for plain vanilla call or put options are simply defined by
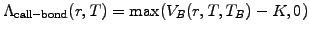 |
|
|
(2.2.4#eq.1) |
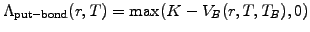 |
|
|
|
Directly related is the
interest rate cap (alt.
floor), which can be understood as a form
of insurance against underlying floating rates moving above (alt. below)
a certain level. Imagine a loan for an amount A, where the a priori unknown floating rate
ri=r(ti,ti +
ti)
resets to LIBOR at the end of every period and leads to payments float(ti+1=Ari+1t
To guarantee that these payments do not exceed (alt. drop below) a certain
level, the loan can be supplemented with a cap (alt. floor), which is itself
composed of a series of
caplets (alt.
floorlets) having all the same cap-/floor rate K,
and paying the difference when the floating rate moves beyond:
No-arbitrage arguments again show that the a priori unknown future values
of the rates resetting at the end of the time interval have to be equal to
the projected forward rates
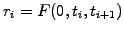 .
Exercise 2.11 shows that a floorlet is closely related with a call option
on a discount bond and a caplet is closely related with the corresponding
put option.
By holding a cap and shorting a floor with different rates Kfloor < Kcap
you get a collar, which guarantees that
the interest rate remain within a pre-determined interval.
Using the same rates Kfloor = Kcap
guarantees the payment of a fixed rate leading to the cap-floor parity
.
Exercise 2.11 shows that a floorlet is closely related with a call option
on a discount bond and a caplet is closely related with the corresponding
put option.
By holding a cap and shorting a floor with different rates Kfloor < Kcap
you get a collar, which guarantees that
the interest rate remain within a pre-determined interval.
Using the same rates Kfloor = Kcap
guarantees the payment of a fixed rate leading to the cap-floor parity
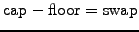 |
(2.2.4#eq.3) |
Options can also be defined on credit derivatives: a European swap option or
swaption carries the right to enter a swap (i.e. switch from variable
to fixed interest rates)
at a predetermined rate K':
where B=åk
P(ti,ti+k)
tk
Options on caps-/floors can be defined in the same manner as above and are
called captions and floortions.
SYLLABUS Previous: 2.2.3 Interest rate swaps
Up: 2.2 The credit market
Next: 2.3 Convertible bonds


 SYLLABUS Previous: 2.2.3 Interest rate swaps
Up: 2.2 The credit market
Next: 2.3 Convertible bonds
SYLLABUS Previous: 2.2.3 Interest rate swaps
Up: 2.2 The credit market
Next: 2.3 Convertible bonds