previous up next SYLLABUS  Previous: 2.2.2 Underlying discount bonds  Up: 2.2 The credit market  Next: 2.2.4 Bond options: caps,


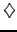
2.2.3 Interest rate swaps and forward rate agreements $ \diamondsuit $

[ SLIDE swap - equilibrium rate - FRA || VIDEO modem - LAN - DSL]


A plain vanilla interest rate swap is a contract whereby two parties agree to exchange, at known dates in the future, a fixed for a floating set of interest rate payments without ever exchanging the notional principal A. The fixed leg of the swap replicates the coupons (1.3#eq.5) payed at the end of every accrual period spanning from the reset time to the payment time [ti;ti+ ti]  

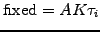$\displaystyle \textrm{fixed}=A K \tau_i$ (2.2.3#eq.1)


using a fixed interest rate K that is initially agreed upon when the swap is purchased. The floating leg consists of payments that also occur at a time ti+1=ti+ ti  

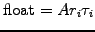$\displaystyle \textrm{float}=A r_i \tau_i$ (2.2.3#eq.2)


using however the unknown spot rate ri=r(ti,ti+1)   that prevails at some future times ti.  

Figure 2.2.3#fig.1: Sketch of an example showing the cash flows when a bank takes the credit risk from a loan taker and agrees to pay 2% in excess of the floating spot rate in exchange of a fixed interet payments of 6%.
\includegraphics[width=10cm]{figs/sketchSwap.eps}

The present value of both legs can be discounted back in time using discount bonds to get
$\displaystyle PV(\textrm{fixed})= A K \tau_i P(t,t_{i+1})$      
$\displaystyle PV(\textrm{float})= A r_i \tau_i P(t,t_{i+1})$   $\displaystyle = A r_i \tau_i \displaystyle{\frac{1}{1+r_i\tau_i}}$ (2.2.3#eq.3)


where a simple compounding has been assumed to substitute the spot rate for the discount bond using (2.2.2#eq.1). Now compare the latter with a portfolio long one bond P(0,ti)   and short another with longer maturity P(0,ti+1). At time i,   the portfolio value is

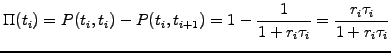$\displaystyle \Pi(t_i)= P(t_i,t_i)-P(t_i,t_{i+1})= 1 - \frac{1}{1+r_i\tau_i} = \frac{r_i \tau_i}{1+r_i\tau_i}$ (2.2.3#eq.4)


or indeed the same, to a normalizing constant A, as the floating leg in (2.2.3#eq.3)

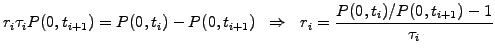$\displaystyle r_i\tau_i P(0,t_{i+1}) = P(0,t_i)-P(0,t_{i+1}) \;\; \Rightarrow \;\; r_i=\frac{P(0,t_i)/P(0,t_{i+1}) -1}{\tau_i}$ (2.2.3#eq.5)


After identification with the definition of simply compounded forward rates (2.2.2#eq.2), this shows that the a priori unknown values of future spot rates have the same value today as the projected forward rates ri=Fi= F(0,ti,ti+1).  


An equilibrium swap rate can therefore be calculated in the form of a weighted average of forward rates, making the values of the floating and the fixed legs equal when the contract is initially written at t=0

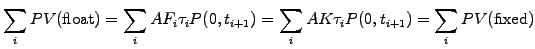$\displaystyle \sum_i PV(\textrm{float})= \sum_i A F_i \tau_i P(0,t_{i+1}) = \sum_i A K \tau_i P(0,t_{i+1}) = \sum_i PV(\textrm{fixed})$ (2.2.3#eq.6)

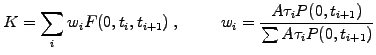$\displaystyle K = \sum_i w_i F(0,t_i,t_{i+1}) \;, \hspace{1cm} w_i = \frac{A \tau_i P(0,t_{i+1})}{\sum A \tau_i P(0,t_{i+1})}$ (2.2.3#eq.7)


Notice that no assumption about the random evolution of spot rates has been made, the combination of long and short bonds being amenable to a purely deterministic evaluation in a manner similar to what was has been found for the put-call parity relation (2.1.3#eq.2). By definition, a one period swap is sometimes called forward rate agreement: an X's/Y's FRA refers to an interest rate swap starting in X and finishing in Y months and has a present value given by the difference between the floating and the fixed legs

$\displaystyle PV(\textrm{FRA})=A[P(0,t_i)-P(0,t_{i+1})] - AK P(0,t_{i+1}) \tau_i$ (2.2.3#eq.8)


The total amount of cash payed after each accrual period [ti;ti+1]   depends on the difference between the settlement rate Ri   and the forward rate K; after a simply compounded discounting, the cash flow at a time ti   from the seller to the buyer amounts to

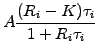$\displaystyle A\frac{(R_i-K)\tau_i}{1+R_i\tau_i}$ (2.2.3#eq.9)


Here is an example showing the entire sequence of events:
Wed 02-Feb-00 2's/5's FRA contract written at 6% for EUR 1 Mio
Fri 31-Mar-00 settlement rate determined at 5% (3 months forward
  LIBOR for the period Tue 04-Apr-00 to Wed 05-Jul-00)
  Settlement amount given by (2.2.3#eq.9)
  1000000 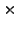$ \times$ (-0.01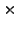$ \times$ 92/360)/(1+0.05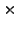$ \times$ 92/360) = - 2523.31
Wed 05-Jul-00 buyer pays seller EUR 2523.31

Beware of the dealers jargon, which is opposite for bonds and swaps: bid means to buy fixed in bonds and sell fixed in swaps, whereas offer means to sell fixed in bonds and buy fixed in swaps.
To conclude this section with a little review, it should now be clear that for the holder of a swap, the earnings increase (alt. drops) when the spot rate evolves above (alt. drops below) the projected forward rates. At the same time, the market data in (1.3#tab.1) illustrates how an increasing spot rate produces a rise in the par coupon (particular coupon that prices the bond today exactly at par - i.e. for a present value equal to the nominal principal) when the bond trades at a discount (alt. premium).

SYLLABUS  Previous: 2.2.2 Underlying discount bonds  Up: 2.2 The credit market  Next: 2.2.4 Bond options: caps,