

 SYLLABUS Previous: 3.3.2 Itô lemma
Up: 3.3 Improved model using
Next: 3.4 Hedging an option
SYLLABUS Previous: 3.3.2 Itô lemma
Up: 3.3 Improved model using
Next: 3.4 Hedging an option
3.3.3 Evaluate an expectancy or eliminate the uncertainty
[ SLIDE
portfolio -
no random -
no arbitrage -
Black-Scholes -
properties ||
VIDEO
modem -
LAN -
DSL]
The Itô lemma shows how it is possible to superpose infinitesimal
increments 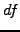 to mimic the evolution of the value of a financial
derivative
to mimic the evolution of the value of a financial
derivative 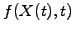 , which is a known function of the stochastic
spot price
, which is a known function of the stochastic
spot price 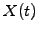 .
Starting from an initial (alt. terminal) value that is known at a
time
.
Starting from an initial (alt. terminal) value that is known at a
time 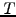 , a finite number of incremental changes
, a finite number of incremental changes 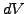 can in be
accumulated to approximate a single possible outcome at a later
(alt. earlier) time: the implementation of the so-called
Monte-Carlo method
will discussed later with a practical example (sect.4.5).
At the end, the fair price for the derivative is calculated as the
expectancy from a large number of possible outcomes, i.e. by
performing a statistical average where each payoff is properly
weighted with the number of times this value has been reached.
can in be
accumulated to approximate a single possible outcome at a later
(alt. earlier) time: the implementation of the so-called
Monte-Carlo method
will discussed later with a practical example (sect.4.5).
At the end, the fair price for the derivative is calculated as the
expectancy from a large number of possible outcomes, i.e. by
performing a statistical average where each payoff is properly
weighted with the number of times this value has been reached.
The main drawback of a statistical method is the slow convergence
(
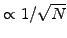 ) with the number of samples. The problem can
be traced back to the difficulty of integrating the stochastic
term in the Itô differential (3.3.2#eq.2).
By combining anti-correlated assets, it is however possible to reduce
the amount of fluctuations in a portfolio. Sometimes, it is even possible
to completely eliminate the uncertainty through delta-hedging,
in effect transforming the stochastic differential equation (SDE) into
a partial differential equation (PDE) that is much simpler to solve.
For that
) with the number of samples. The problem can
be traced back to the difficulty of integrating the stochastic
term in the Itô differential (3.3.2#eq.2).
By combining anti-correlated assets, it is however possible to reduce
the amount of fluctuations in a portfolio. Sometimes, it is even possible
to completely eliminate the uncertainty through delta-hedging,
in effect transforming the stochastic differential equation (SDE) into
a partial differential equation (PDE) that is much simpler to solve.
For that
- Create a portfolio, combining one derivative (e.g. an option) of
value
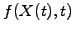 with a yet unspecified, but constant number
with a yet unspecified, but constant number 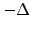 of the underlying asset. The initial value of this portfolio and its
incremental change per time-step are
of the underlying asset. The initial value of this portfolio and its
incremental change per time-step are
 |
(3.3.3#eq.1) |
where the Itô differential (3.3.2#eq.2) can be used to substitute 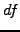 and the stochastic differential (3.3.1#eq.1) for
and the stochastic differential (3.3.1#eq.1) for 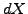 .
.
- Choose the right amount
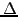 of the underlying so as to exactly
cancel the random component, which is proportional to
of the underlying so as to exactly
cancel the random component, which is proportional to 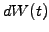 in the
Itô differential
in the
Itô differential
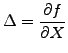 |
(3.3.3#eq.2) |
With this choice, the total value of the portfolio becomes deterministic,
i.e. the remaining equation has no term left in 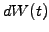 .
.
- No-arbitrage arguments show that without taking any risk, the
portfolio has to earn the same as the risk-free interest rate
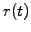
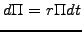 |
(3.3.3#eq.3) |
Indeed, if this was not the case and the earnings were larger (alt. smaller),
arbitrageurs would immediately borrow money from (alt. lend money to) the
market until the derivative expires and make a risk less profit from the
difference in the returns.
- Reassemble the small deterministic incremental values into a partial
differential equation, which can be solved more efficiently to obtain the
present value of the derivative
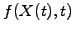 .
.
Of course, the amount 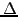 will change after a short time and the
portfolio has to be continuously re-hedged to obtain a meaningful
value for the derivative-which is not quite possible in the real world.
Two examples illustrate the procedure in the coming sections, using
delta-hedging to calculate the price of derivatives in the stock and
the bond markets.
will change after a short time and the
portfolio has to be continuously re-hedged to obtain a meaningful
value for the derivative-which is not quite possible in the real world.
Two examples illustrate the procedure in the coming sections, using
delta-hedging to calculate the price of derivatives in the stock and
the bond markets.
SYLLABUS Previous: 3.3.2 Itô lemma
Up: 3.3 Improved model using
Next: 3.4 Hedging an option


 SYLLABUS Previous: 3.3.2 Itô lemma
Up: 3.3 Improved model using
Next: 3.4 Hedging an option
SYLLABUS Previous: 3.3.2 Itô lemma
Up: 3.3 Improved model using
Next: 3.4 Hedging an option