

 SYLLABUS Previous: 3.4 Hedging an option
Up: 3 FORECASTING WITH UNCERTAINTY
Next: 3.6 Computer quiz
SYLLABUS Previous: 3.4 Hedging an option
Up: 3 FORECASTING WITH UNCERTAINTY
Next: 3.6 Computer quiz
3.5 Hedging a bond with another bond (Vasicek)
[ SLIDE
Ito -
no random -
no arbitrage -
Vasicek -
price of risk ||
VIDEO
modem -
LAN -
DSL]
In contrast to the price of a share (which can never drop below zero
because of the regulations of bankruptcies), it is in principle
possible to live with negative interest rates: these have even been
observed in Switzerland in the 1960s, albeit only for a short period.
This motivates the development of stochastic models for long term
interest rates where the random walk of the spot rate increments 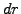 is based on (3.3.1#eq.1) and the distribution chosen somewhere between
is based on (3.3.1#eq.1) and the distribution chosen somewhere between
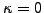 (normal walk assumed by Vasicek [23]) and
(normal walk assumed by Vasicek [23]) and
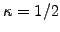 (assumed by Cox, Ingersoll and Ross [5]).
(assumed by Cox, Ingersoll and Ross [5]).
Here we follow the classical derivation from Vasicek using 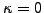 and apply Itô's lemma to calculate the stochastic price increment
for a bond
and apply Itô's lemma to calculate the stochastic price increment
for a bond 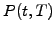 of maturity
of maturity 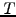
![$\displaystyle dP(t,T)= \underbrace{ \left[ \frac{\partial P}{\partial t} +\frac...
...erbrace{\left[\sigma_s\frac{\partial P}{\partial r}\right]}_{\sigma(t,T)} dW(t)$](s3img144.gif) |
(3.5#eq.1) |
The drift and volatility of a bond
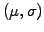 depend on the spot rate
depend on the spot rate
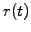 and can be parametrized using market data
and can be parametrized using market data
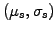 .
Having no anti-correlated underlying as for the case of stock options, the
trick here is to create here a portfolio that is long one bond
.
Having no anti-correlated underlying as for the case of stock options, the
trick here is to create here a portfolio that is long one bond 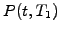 and short a number
and short a number 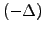 of bonds
of bonds 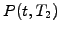 with a different
maturity
with a different
maturity 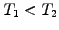 . The portfolio value and its incremental change per
time step become
. The portfolio value and its incremental change per
time step become
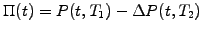 |
(3.5#eq.2) |
![$\displaystyle d\Pi(t)= \left[ \mu(t,T_1) -\Delta \mu(t,T_2)\right] dt +\left[ \sigma(t,T_1) -\Delta \sigma(t,T_2)\right] dW(t)$](s3img151.gif) |
(3.5#eq.3) |
Choosing
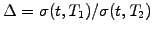 to eliminate the random
component, the portfolio becomes deterministic and, using no-arbitrage
arguments, earns exactly the risk-free spot rate
to eliminate the random
component, the portfolio becomes deterministic and, using no-arbitrage
arguments, earns exactly the risk-free spot rate
![$\displaystyle d\Pi(t) = dP(t,T_1)- \Delta dP(t,T_2) = r(t)\Pi(t)dt = r(t)dt\left[ P(t,T_1)- \Delta P(t,T_2)\right]$](s3img153.gif) |
(3.5#eq.4) |
Substitute the value for  , insert (3.5#eq.1) for the
increments and move all the terms with the same maturity on the
same side of the equation to obtain
, insert (3.5#eq.1) for the
increments and move all the terms with the same maturity on the
same side of the equation to obtain
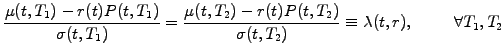 |
(3.5#eq.5) |
This shows that the so-called
market price of risk
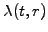 is independent of the maturity and can therefore
be used to parameterize the market.
Rewriting the bond drift
is independent of the maturity and can therefore
be used to parameterize the market.
Rewriting the bond drift 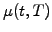 in (3.5#eq.1) in terms of the
market price of risk (3.5#eq.5), the properly hedged portfolio
(3.5#eq.2) finally yields the bond pricing equation
in (3.5#eq.1) in terms of the
market price of risk (3.5#eq.5), the properly hedged portfolio
(3.5#eq.2) finally yields the bond pricing equation
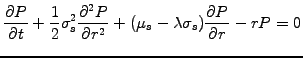 |
(3.5#eq.6) |
which can be solved using the normalized terminal payoff at maturity
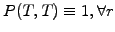 as the terminal condition.
Boundary conditions depend on the model for the spot rate, e.g.
as the terminal condition.
Boundary conditions depend on the model for the spot rate, e.g.
which can be used with
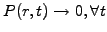 when
when
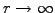 and keeping
and keeping 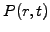 finite for small
finite for small 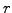 .
.
Using (3.5#eq.6) to re-write the deterministic component of a
single bond (3.5#eq.1), Itô's lemma can be put into another form
![$\displaystyle dP = \left[ \lambda\sigma_s \frac{\partial P}{\partial r} + rP \right] dt + \sigma_s\frac{\partial P}{\partial r} dW(t)$](s3img166.gif) |
(3.5#eq.8) |
or
![$\displaystyle dP -rPdt = \sigma_s\frac{\partial P}{\partial r} \left[ \lambda dt + dW(t) \right]$](s3img167.gif) |
(3.5#eq.9) |
showing on the left hand side that a higher return can be earned exceeding
the risk-free interest rates, provided that the investor accepts a certain
level of risk 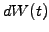 . Indeed, the portfolio grows by an extra
. Indeed, the portfolio grows by an extra
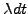 per unit of risk
per unit of risk 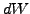 .
This justifies the interpretation of
.
This justifies the interpretation of 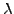 as the market price of risk,
with investors that are either risk seeking or risk averse depending whether
as the market price of risk,
with investors that are either risk seeking or risk averse depending whether
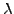 is positive or negative.
is positive or negative.
SYLLABUS Previous: 3.4 Hedging an option
Up: 3 FORECASTING WITH UNCERTAINTY
Next: 3.6 Computer quiz


 SYLLABUS Previous: 3.4 Hedging an option
Up: 3 FORECASTING WITH UNCERTAINTY
Next: 3.6 Computer quiz
SYLLABUS Previous: 3.4 Hedging an option
Up: 3 FORECASTING WITH UNCERTAINTY
Next: 3.6 Computer quiz