

 ','..','$myPermit') ?>
SYLLABUS Previous: 6.1 American stock options
Up: 6.1 American stock options
Next: 6.1.2 Parameters illustrated with
','..','$myPermit') ?>
SYLLABUS Previous: 6.1 American stock options
Up: 6.1 American stock options
Next: 6.1.2 Parameters illustrated with
6.1.1 The American Black-Scholes model for dummies
[ SLIDE
American payoff -
experiments ||
VIDEO
99) echo "
modem -
LAN -
DSL
"; else echo "login";?>
]
Since an American option confers its holder the right to buy or sell
an underlying share 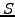 any time up to the expiry date, the option
price
any time up to the expiry date, the option
price 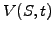 can never drop below the
intrinsic value
that has been defined in sect.2.1.3.
Indeed, if the price dropped below, a crowd of arbitragers would
immediately seize the opportunity and buy a large amount of
options only to exercise them immediately for a risk less profit
can never drop below the
intrinsic value
that has been defined in sect.2.1.3.
Indeed, if the price dropped below, a crowd of arbitragers would
immediately seize the opportunity and buy a large amount of
options only to exercise them immediately for a risk less profit
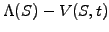 .
The VMARKET applet below illustrates
this with an American put option, where the price never drops below
the intrinsic value even in the presence of a finite interest rate.
.
The VMARKET applet below illustrates
this with an American put option, where the price never drops below
the intrinsic value even in the presence of a finite interest rate.
VMARKET applet: press Start/Stop
to calculate the price of an American put option struck for 10 EUR
up to 9 months before the expiry, in a market with 40% volatility
and a spot rate of 3%.
The black (alt. grey) line shows the present (alt. intrinsic) value of
the option V(S,t) for a range of underlying prices 0 < S < 20,
as the time runs from the expiry date (T=0) back to three quarter of
a year (T-t=0.75) before the expiry date.
|
|
"; ?>
Since the price necessarily exceeds the
intrinsic value,
American options never develop the
negative time value
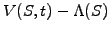 that has previously been observed
for European options.
In fact, the experiments above suggest that a crude estimate for
the value of an American option can be obtained simply by choosing
whichever is larger, the European Black-Scholes formula or the
intrinsic value
that has previously been observed
for European options.
In fact, the experiments above suggest that a crude estimate for
the value of an American option can be obtained simply by choosing
whichever is larger, the European Black-Scholes formula or the
intrinsic value
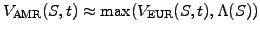 |
(6.1.1#eq.1) |
Discontinuities where the European payoff intersects the intrinsic
value are in contradiction with the efficient market hypothesis: indeed,
delta-hedging strategies exist from which risk-free
profits can be made and arbitragers quickly smooth out the transition.
This shows that the approximation (6.1.1#eq.1) is not in general
sufficient for the pricing of American options, but it can nevertheless
be useful when an explicit formula is needed.
SYLLABUS Previous: 6.1 American stock options
Up: 6.1 American stock options
Next: 6.1.2 Parameters illustrated with


 ','..','$myPermit') ?>
SYLLABUS Previous: 6.1 American stock options
Up: 6.1 American stock options
Next: 6.1.2 Parameters illustrated with
','..','$myPermit') ?>
SYLLABUS Previous: 6.1 American stock options
Up: 6.1 American stock options
Next: 6.1.2 Parameters illustrated with
![]() any time up to the expiry date, the option
price
any time up to the expiry date, the option
price ![]() can never drop below the
intrinsic value
that has been defined in sect.2.1.3.
Indeed, if the price dropped below, a crowd of arbitragers would
immediately seize the opportunity and buy a large amount of
options only to exercise them immediately for a risk less profit
can never drop below the
intrinsic value
that has been defined in sect.2.1.3.
Indeed, if the price dropped below, a crowd of arbitragers would
immediately seize the opportunity and buy a large amount of
options only to exercise them immediately for a risk less profit
![]() .
The VMARKET applet below illustrates
this with an American put option, where the price never drops below
the intrinsic value even in the presence of a finite interest rate.
.
The VMARKET applet below illustrates
this with an American put option, where the price never drops below
the intrinsic value even in the presence of a finite interest rate.
![]() that has previously been observed
for European options.
In fact, the experiments above suggest that a crude estimate for
the value of an American option can be obtained simply by choosing
whichever is larger, the European Black-Scholes formula or the
intrinsic value
that has previously been observed
for European options.
In fact, the experiments above suggest that a crude estimate for
the value of an American option can be obtained simply by choosing
whichever is larger, the European Black-Scholes formula or the
intrinsic value