

 SYLLABUS Previous: 6.2 Methods for American
Up: 6.2 Methods for American
Next: 6.2.2 Solution of the
SYLLABUS Previous: 6.2 Methods for American
Up: 6.2 Methods for American
Next: 6.2.2 Solution of the
6.2.1 The Black-Scholes equation for American options
[ SLIDE
SDE -
Black-Scholes ||
VIDEO
modem -
LAN -
DSL]
Following the same procedure as in chapter 3, the Black-Scholes
model is first extended to account for the possibility of exercising the
American option anytime up to the expiry.
Allowing for a continuous dividend payment at a rate 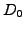 , the random
walk for the underlying price increment (3.3.1#eq.1) is modified to
, the random
walk for the underlying price increment (3.3.1#eq.1) is modified to
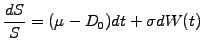 |
(6.2.1#eq.1) |
Create a portfolio combining an American option with a number 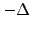 of shares and store the earnings from a dividend yield.
The initial value and the incremental change are
of shares and store the earnings from a dividend yield.
The initial value and the incremental change are
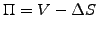 |
(6.2.1#eq.2) |
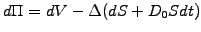 |
(6.2.1#eq.3) |
Using Itô's lemma (3.3.2#eq.2) to calculate the stochastic increment
in the option value 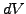 as a function of the underlying, the random
component is again eliminated by continuously re-hedging the portfolio
with a number
as a function of the underlying, the random
component is again eliminated by continuously re-hedging the portfolio
with a number
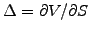 of shares.
No arbitrage arguments show that without taking any risk, the portfolio
can at most earn the risk-free return of the spot rate.
Because an American option can be exercised any time until it expires, the
incremental change in the portfolio value satisfies the inequality
of shares.
No arbitrage arguments show that without taking any risk, the portfolio
can at most earn the risk-free return of the spot rate.
Because an American option can be exercised any time until it expires, the
incremental change in the portfolio value satisfies the inequality
![$\displaystyle d\Pi=\left[ \frac{\partial V}{\partial t} +\frac{1}{2}\sigma^2 S^...
...l^2 V}{\partial S^2} -D_0 S\frac{\partial V}{\partial S} \right] dt \le r\Pi dt$](s6img53.gif) |
(6.2.1#eq.4) |
which leads directly to Black-Scholes equation for American options
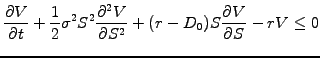 |
(6.2.1#eq.5) |
In addition to the usual boundary and terminal condition
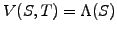 ,
this inequality (known in mathematics as an
obstacle problem)
must be supplemented by the free boundary condition
,
this inequality (known in mathematics as an
obstacle problem)
must be supplemented by the free boundary condition
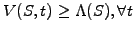 .
Apart from that, the Black-Scholes equation is the same for European
options paying a dividend with the strict equality here replaced by
an inequality.
The same change of variables (4.3.1#eq.1,4.3.1#eq.4) can therefore
be used to transform the problem to log-normal variables
.
Apart from that, the Black-Scholes equation is the same for European
options paying a dividend with the strict equality here replaced by
an inequality.
The same change of variables (4.3.1#eq.1,4.3.1#eq.4) can therefore
be used to transform the problem to log-normal variables 
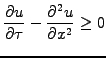 |
(6.2.1#eq.6) |
keeping in mind that the solution has to satisfy the corresponding
free-boundary condition of the form
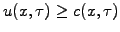 .
.
SYLLABUS Previous: 6.2 Methods for American
Up: 6.2 Methods for American
Next: 6.2.2 Solution of the


 SYLLABUS Previous: 6.2 Methods for American
Up: 6.2 Methods for American
Next: 6.2.2 Solution of the
SYLLABUS Previous: 6.2 Methods for American
Up: 6.2 Methods for American
Next: 6.2.2 Solution of the