

 SYLLABUS Previous: 2.2.2 Underlying discount bonds
Up: 2.2 The credit market
Next: 2.2.4 Bond options: caps,
SYLLABUS Previous: 2.2.2 Underlying discount bonds
Up: 2.2 The credit market
Next: 2.2.4 Bond options: caps,
2.2.3 Interest rate swaps and forward rate agreements
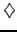
[ SLIDE
swap -
equilibrium rate -
FRA ||
VIDEO
modem -
LAN -
DSL]
A plain vanilla interest rate swap is a
contract whereby two parties agree to exchange, at known dates in the
future, a fixed for a floating set of interest rate payments without ever
exchanging the notional principal A.
The fixed leg of the swap replicates the
coupons (1.3#eq.5) payed at the end
of every accrual period spanning
from the reset time to the
payment time [ti;ti+
ti]
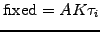 |
(2.2.3#eq.1) |
using a fixed interest rate K that is initially agreed upon when the
swap is purchased.
The floating leg consists of payments
that also occur at a time ti+1=ti+
ti
 |
(2.2.3#eq.2) |
using however the unknown spot rate ri=r(ti,ti+1)
that prevails at some future times ti.
Figure 2.2.3#fig.1:
Sketch of an example showing the cash flows when a bank takes the
credit risk from a loan taker and agrees to pay 2% in excess of the
floating spot rate in exchange of a fixed interet payments of 6%.
|
|
The present value of both legs can be discounted back in time using
discount bonds to get
where a simple compounding has been assumed to substitute the
spot rate for the discount bond using (2.2.2#eq.1).
Now compare the latter with a portfolio long one bond P(0,ti)
and short another with longer maturity P(0,ti+1). At time i,
the portfolio value is
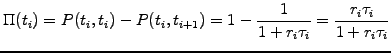 |
(2.2.3#eq.4) |
or indeed the same, to a normalizing constant A, as the floating leg
in (2.2.3#eq.3)
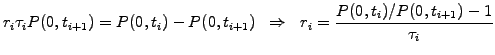 |
(2.2.3#eq.5) |
After identification with the definition of simply compounded forward
rates (2.2.2#eq.2), this shows that the a priori unknown values of
future spot rates have the same value today as the projected forward
rates ri=Fi=
F(0,ti,ti+1).
An equilibrium swap rate
can therefore be calculated in the form of a weighted average of forward
rates, making the values of the floating and the fixed legs equal when
the contract is initially written at t=0
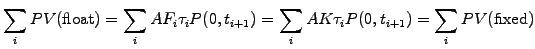 |
(2.2.3#eq.6) |
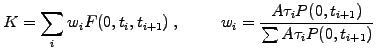 |
(2.2.3#eq.7) |
Notice that no assumption about the random evolution of spot rates has
been made, the combination of long and short bonds being amenable to a
purely deterministic evaluation in a manner similar to what was has
been found for the put-call parity relation (2.1.3#eq.2).
By definition, a one period swap is sometimes called
forward rate agreement: an X's/Y's FRA refers
to an interest rate swap starting in X and finishing in Y months and has
a present value given by the difference between the floating and the
fixed legs
![$\displaystyle PV(\textrm{FRA})=A[P(0,t_i)-P(0,t_{i+1})] - AK P(0,t_{i+1}) \tau_i$](s2img115.gif) |
(2.2.3#eq.8) |
The total amount of cash payed after each accrual period [ti;ti+1]
depends on the difference between the settlement rate Ri
and the forward rate K; after a simply compounded discounting, the cash flow
at a time ti
from the seller to the buyer amounts to
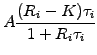 |
(2.2.3#eq.9) |
Here is an example showing the entire sequence of events:
| Wed 02-Feb-00 |
2's/5's FRA contract written at 6% for EUR 1 Mio |
| Fri 31-Mar-00 |
settlement rate determined at 5% (3 months forward |
| |
LIBOR for the period Tue 04-Apr-00 to Wed 05-Jul-00) |
| |
Settlement amount given by (2.2.3#eq.9) |
| |
1000000 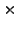 (-0.01
(-0.01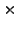 92/360)/(1+0.05
92/360)/(1+0.05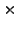 92/360)
= - 2523.31
92/360)
= - 2523.31 |
| Wed 05-Jul-00 |
buyer pays seller EUR 2523.31 |
Beware of the dealers jargon, which is opposite for bonds and swaps:
bid means to buy fixed in bonds and sell
fixed in swaps, whereas offer means to
sell fixed in bonds and buy fixed in swaps.
To conclude this section with a little review, it should now be clear that
for the holder of a swap, the earnings increase (alt. drops) when the spot
rate evolves above (alt. drops below) the projected forward rates.
At the same time, the market data in (1.3#tab.1) illustrates how an
increasing spot rate produces a rise in the par coupon (particular
coupon that prices the bond today exactly at par
- i.e. for a present value equal to the nominal principal) when the bond
trades at a discount
(alt. premium).
SYLLABUS Previous: 2.2.2 Underlying discount bonds
Up: 2.2 The credit market
Next: 2.2.4 Bond options: caps,


 SYLLABUS Previous: 2.2.2 Underlying discount bonds
Up: 2.2 The credit market
Next: 2.2.4 Bond options: caps,
SYLLABUS Previous: 2.2.2 Underlying discount bonds
Up: 2.2 The credit market
Next: 2.2.4 Bond options: caps,
![\includegraphics[width=10cm]{figs/sketchSwap.eps}](s2img107.gif)
(-0.01
92/360)/(1+0.05
92/360) = - 2523.31