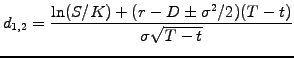SYLLABUS Previous: 4.3.2 Solution of the
Up: 4.3 Methods for European
Next: 4.4 Methods for European
SYLLABUS Previous: 4.3.2 Solution of the
Up: 4.3 Methods for European
Next: 4.4 Methods for European
4.3.3 Black-Scholes formula
[ SLIDE
formula -
N(x) || same
VIDEO as previous section
modem -
LAN -
DSL]
In the case of plain vanilla call and put options, the price can be
evaluated in terms of the cumulative normal distribution 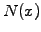 and
yields the well known Black-Scholes formula
and
yields the well known Black-Scholes formula
![$\displaystyle V_\mathrm{call}(S,t)=SN(d_1)-K\exp[-r(T-t)]N(d_2)$](s4img113.gif) |
(4.3.3#eq.1) |
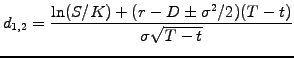 |
(4.3.3#eq.2) |
![$\displaystyle V_\mathrm{put}(S,t)-V_\mathrm{call}(S,t)+S=K\exp[-r(T-t)]$](s4img115.gif) |
(4.3.3#eq.3) |
Remember that 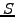 denotes the (spot) price of an underlying share that
pays a dividend
denotes the (spot) price of an underlying share that
pays a dividend 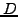 and has a historical volatility
and has a historical volatility 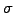 ,
, 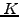 is
the strike price of the option evolving in time
is
the strike price of the option evolving in time ![$ t\in[0;T]$](s4img117.gif) from the
present to the expiry date and
from the
present to the expiry date and 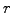 the risk-free interest (spot) rate.
Note that the last relation (4.3.3#eq.3) is nothing more
than the put-call parity previously obtained in (2.1.3#eq.2),
where the guaranteed payoff has been discounted back in time to achieve
the risk free return of the spot rate.
The cumulative normal distribution is related with the so-called error
function
the risk-free interest (spot) rate.
Note that the last relation (4.3.3#eq.3) is nothing more
than the put-call parity previously obtained in (2.1.3#eq.2),
where the guaranteed payoff has been discounted back in time to achieve
the risk free return of the spot rate.
The cumulative normal distribution is related with the so-called error
function
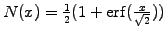 , which
is available in Matlab and can be approximated with 6 digits
accuracy using the polynomial expansion [1]
, which
is available in Matlab and can be approximated with 6 digits
accuracy using the polynomial expansion [1]
with the coefficients
g=0.2316419, a1=0.319381530,
a2=-0.356563782, a3=1.781477937,
a4=-1.821255978, a5=1.330274429.
SYLLABUS Previous: 4.3.2 Solution of the
Up: 4.3 Methods for European
Next: 4.4 Methods for European


 SYLLABUS Previous: 4.3.2 Solution of the
Up: 4.3 Methods for European
Next: 4.4 Methods for European
SYLLABUS Previous: 4.3.2 Solution of the
Up: 4.3 Methods for European
Next: 4.4 Methods for European