

 SYLLABUS Previous: 4.3.1 Transformation to log-normal
Up: 4.3 Methods for European
Next: 4.3.3 Black-Scholes formula
SYLLABUS Previous: 4.3.1 Transformation to log-normal
Up: 4.3 Methods for European
Next: 4.3.3 Black-Scholes formula
4.3.2 Solution of the normalized diffusion equation
[ SLIDE Fourier-Laplace
fwd -
bck || Solution
binary options || same
VIDEO as previous section:
modem -
LAN -
DSL]
Readers interested in solving the diffusion equation (4.3.1#eq.5)
analytically are likely to be familiar with the Fourier-Laplace transform
that is commonly used to solve initial and boundary value problems.
Others may skip the whole derivation and verify that the final result
(4.3.2#eq.11) indeed satisfies the Black-Scholes equation (3.4#eq.4).
Start by transforming (4.3.1#eq.5) with a Laplace transform in time
![$\displaystyle \int_0^\infty d\tau \exp(i\omega \tau)\left[ \pd{u}{\tau} -\pd{^2 u}{x^2} \right] = 0, \qquad \Im m(\omega)>0$](s4img92.gif) |
(4.3.2#eq.1) |
Note that the condition
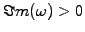 is important to ensure causality.
Integrate the first term by parts and substitute a Dirac function
is important to ensure causality.
Integrate the first term by parts and substitute a Dirac function
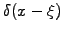 for the initial condition
for the initial condition 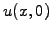
![\begin{displaymath}\begin{split}\left. u\exp(i\omega \tau) \right\vert _0^\infty...
... u(x,\omega) -\pd{^2 u(x,\omega)}{x^2} \right] &= 0 \end{split}\end{displaymath}](s4img95.gif) |
(4.3.2#eq.2) |
The notation
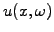 refers to the Laplace transform of
refers to the Laplace transform of 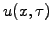 .
Spatial derivatives are dealt with a Fourier transform
.
Spatial derivatives are dealt with a Fourier transform
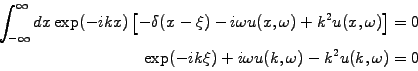 |
(4.3.2#eq.3) |
and yields an explicit solution in Fourier-Laplace space
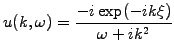 |
(4.3.2#eq.4) |
The pole in the complex plane for
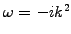 needs to be taken
into account when inverting the Laplace transform in a causal manner
needs to be taken
into account when inverting the Laplace transform in a causal manner
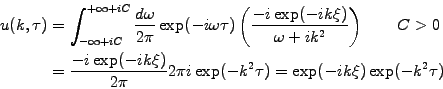 |
(4.3.2#eq.5) |
where the residue theorem has been used to evaluate the complex integral,
closing the contour in the lower half plane where the phase factor
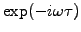 decays exponentially.
Invert the Fourier transformation
decays exponentially.
Invert the Fourier transformation
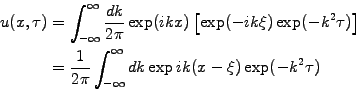 |
(4.3.2#eq.6) |
and use the formula (3.323.2) from Gradshteyn & Ryzhik [9]
![$\displaystyle \int_{-\infty}^{\infty} dx \exp(-p^2x^2)\exp(\pm qx) = \frac{\sqrt{\pi}}{p}\exp\left[\frac{q^2}{4p^2}\right] \qquad p>0$](s4img104.gif) |
(4.3.2#eq.7) |
here with
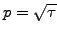 and
and
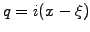 to write down a solution of the
diffusion equation
to write down a solution of the
diffusion equation
![$\displaystyle u(x,\tau)=\frac{1}{2\sqrt{\pi \tau}}\exp\left[-\frac{(x-\xi)^2}{4\tau}\right]$](s4img107.gif) |
(4.3.2#eq.8) |
This shows that a Dirac function
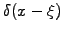 assumed as initial
condition in (4.3.2#eq.2) spreads out into a Gaussian as
time evolves forward.
A superposition of a whole series of Dirac functions can now be
used to decompose any arbitrary initial condition
assumed as initial
condition in (4.3.2#eq.2) spreads out into a Gaussian as
time evolves forward.
A superposition of a whole series of Dirac functions can now be
used to decompose any arbitrary initial condition 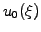
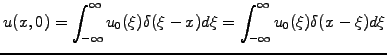 |
(4.3.2#eq.9) |
and after evolving each Dirac functions separately using
(4.3.2#eq.8), can again be superposed at a later
time when 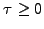 :
:
![$\displaystyle u(x,\tau)=\frac{1}{2\sqrt{\pi \tau}}\int_{-\infty}^\infty d\xi u_0(\xi)\exp\left[-\frac{(\xi-x)^2}{4\tau}\right]$](s4img110.gif) |
(4.3.2#eq.10) |
Transforming back into financial variables (4.3.1#eq.1), some
algebra finally yields a general formula for the price of a binary
option with a terminal payoff
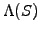
![$\displaystyle V(S,t)=\frac{\exp[-r(T-t)]}{\sigma\sqrt{2\pi(T-t)}} \int_0^\infty...
...) -(r-D-\frac{\sigma^2}{2})(T-t)\right)^2} {2\sigma^2(T-t)} \right]\frac{dX}{X}$](s4img111.gif) |
(4.3.2#eq.11) |
SYLLABUS Previous: 4.3.1 Transformation to log-normal
Up: 4.3 Methods for European
Next: 4.3.3 Black-Scholes formula


 SYLLABUS Previous: 4.3.1 Transformation to log-normal
Up: 4.3 Methods for European
Next: 4.3.3 Black-Scholes formula
SYLLABUS Previous: 4.3.1 Transformation to log-normal
Up: 4.3 Methods for European
Next: 4.3.3 Black-Scholes formula
![$\displaystyle \int_0^\infty d\tau \exp(i\omega \tau)\left[ \pd{u}{\tau} -\pd{^2 u}{x^2} \right] = 0, \qquad \Im m(\omega)>0$](s4img92.gif)
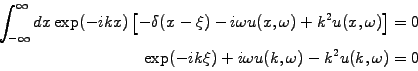
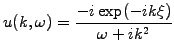
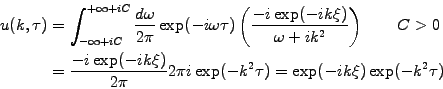
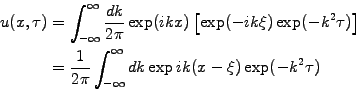
![$\displaystyle \int_{-\infty}^{\infty} dx \exp(-p^2x^2)\exp(\pm qx) = \frac{\sqrt{\pi}}{p}\exp\left[\frac{q^2}{4p^2}\right] \qquad p>0$](s4img104.gif)
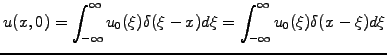
![$\displaystyle u(x,\tau)=\frac{1}{2\sqrt{\pi \tau}}\int_{-\infty}^\infty d\xi u_0(\xi)\exp\left[-\frac{(\xi-x)^2}{4\tau}\right]$](s4img110.gif)