previous up next SYLLABUS  Previous: 4.5.1 Forecast possible realizations  Up: 4.5 Methods for European  Next: 4.6 Computer quiz


4.5.2 Expected value of an option from sampled data $ \spadesuit$

[ SLIDE open - scheme - code || same VIDEO as previous section: modem - LAN - DSL]


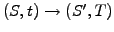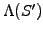To develop your intuition, let us first define the transition probability $ p[S,t;S^\prime,T]$ measuring the likelyhood that an asset evolves from the present value to the terminal value $ (S,t) \rightarrow (S^\prime,T)$ : weighted by the terminal payoff of an option $ \Lambda(S^\prime)$ , this can be used to evaluate the expected return from a particular realisation of the market. Summing the weighted returns from all possible realisations with the proper Jacobian, the present value of an option could be calculated from

$\displaystyle V(S,t) = \exp[-r(T-t)]\int_0^\infty p[S,t;S^\prime,T] \Lambda(S^\prime) \frac{dS^\prime}{{S^\prime}^\kappa}$ (4.5.2#eq.1)


where the expected terminal payoff has been discounted back to the present time 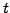$ t$ by multiplication of the factor $ \exp[-r(T-t)]$ . 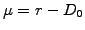This expression can be identified with the analytical solution (4.3.2#eq.11) and shows that the price of an option can also be calculated as the present value of the expected return, using a random walk in a risk-neutral world where the drift is replaced by the spot rate minus the dividend yield $ \mu=r-D_0$ . (Note the analogy with the delta hedging, where the risk has been eliminated to obtain a Black-Scholes equation that is also independent of the drift $ \mu$ .)
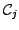
Instead of calculating a complicated n-dimensional path-dependent integral with transition probabilities $ p[S_i,t_i;S_j,t_j\vert\mathcal{C}_j]$ that are subject to multiple conditions $ \mathcal{C}_j$

\begin{displaymath}\begin{split}V(S,t) = \exp[-r(T-t)] &\int_0^\infty \frac{dS_1... ...{n-1},t_{n-1};S_n,T\vert\mathcal{C}_n] \Lambda(S_n) \end{split}\end{displaymath} (4.5.2#eq.2)


the Monte-Carlo sampling method simply uses a large number of possible realizations as an unbiased estimator for the mean price payed when the option is exercised

$\displaystyle V(S,t) = \exp[-r(T-t)]\frac{1}{N}\sum_{k=1}^N \Lambda(S_k)$ (4.5.2#eq.3)


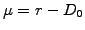The realizations of the underlying asset prices $ \{S_1,S_2,\dots S_N\}$ are evolved using a risk-neutral random walk by setting the drift $ \mu=r-D_0$ . Path dependent features such as barriers can be easily be incorporated at the end, by retaining only those prices that satisfy the conditions: the terminal payoff can for example be multiplied with a marker variable that is either equal to zero or one depending whether the condition has been fulfilled or not. The scheme that has been implemented in the VMARKET class MCSSolution.java reads 
    } else if(Math.abs(kappa-1.)<0.001){        //Separable log-normal
       if (markers){
         for (k=0; k<numberOfRealisations; k++){
           f[j]+= option.getValue(currentState[k][0] *x[j]/strike) *mark[k][0];
           g[j]+= option.getValue(currentState[k][0] *x[j]/strike);
         }
       } else
         for (k=0; k<numberOfRealisations; k++)
           f[j]+= option.getValue(currentState[k][0] *x[j]/strike);
    }
    f[j]=Math.exp(-time*rate)*f[j]/numberOfRealisations;
    g[j]=Math.exp(-time*rate)*g[j]/numberOfRealisations;
If the problem is separable, the random walk is first scaled according to (4.5.1#eq.2) to obtain the terminal value of the underlying 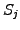$ S_j$ with currentState[k][0]*x[j]/strike; this is then used as an argument to accumulate the terminal payoff 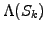$ \Lambda(S_k)$ from every realization using the statement f[j]+=option.getValue() and finally calculate the discounted average of (4.5.2#eq.3) using the last two lines. Note that two functions (f[j],g[j]) have been used to compare the price obtained with-/out barriers. The VMARKET applet below illustrates the result in the case of a simple vanilla put option.

VMARKET applet:  press Start/Stop to simulate the price of a super-share option assuming first a separable log-normal random walk.




Virtual market experiments: Monte-Carlo expectation
  1. Adjust the number of Walkers to achieve a precision of only about 10%.
  2. Change the parameter LogNkappa=1.002 to keep a nearly log-normal distribution of the increments and yet force the applet to use a new random walk for every value of the underlying asset. The ``noise'' between adjacent prices can then be used as a measure or the precision of the calculation. How far were you from the previous 10% target?
  3. Vary the parameter LogNkappa to study how different distributions of the market increments affect the price of an option.



To conclude this section with a comparison between the finite difference and Monte-Carlo methods, remember that Monte-Carlo simulations offer considerable flexibility to model path-dependent options and change the statistics of the market increments. This flexibility, however, comes at a high computing cost for reaching an acceptable precision at the percent level, this even if it is generally sufficient to calculate a single price for the option, which finite differences cannot do.

SYLLABUS  Previous: 4.5.1 Forecast possible realizations  Up: 4.5 Methods for European  Next: 4.6 Computer quiz