

 ','..','$myPermit') ?>
SYLLABUS Previous: 4.1.1 The European Black-Scholes
Up: 4.1 Plain vanilla stock
Next: 4.1.3 Application, time value
','..','$myPermit') ?>
SYLLABUS Previous: 4.1.1 The European Black-Scholes
Up: 4.1 Plain vanilla stock
Next: 4.1.3 Application, time value
4.1.2 Parameters illustrated with VMARKET experiments
[ SLIDE
parameters -
volatility -
rate -
dividend ||
VIDEO
99) echo "
modem -
LAN -
DSL
"; else echo "login";?>
]
Apart from the terminal conditions that specify
the value of an option when it expires (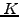 for a vanilla option or
StrikePrice in the applet) and the
numerical parameters that specify the
precision of the calculation (such as the TimeStep,
Walkers and MeshPoints), the Black-Scholes model depends
on only four financial parameters:
for a vanilla option or
StrikePrice in the applet) and the
numerical parameters that specify the
precision of the calculation (such as the TimeStep,
Walkers and MeshPoints), the Black-Scholes model depends
on only four financial parameters:
- The time to the expiry (
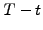 or
RunTime) is usually expressed in a fraction of a year, e.g.
0.25 for three months or a quarter of year to the expiry date.
or
RunTime) is usually expressed in a fraction of a year, e.g.
0.25 for three months or a quarter of year to the expiry date.
- The short term interest or spot rate
(
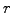 or SpotRate) is specified as a annual fraction of
the capital investment, e.g. 0.05 for a risk free return of five
percent per year.
or SpotRate) is specified as a annual fraction of
the capital investment, e.g. 0.05 for a risk free return of five
percent per year.
- the dividend yield (
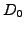 or
Dividend), here modeled with a continuous payment that is
proportional to the underlying price, e.g. 0.04 for a dividend
paying four percent of the share value during one year,
or
Dividend), here modeled with a continuous payment that is
proportional to the underlying price, e.g. 0.04 for a dividend
paying four percent of the share value during one year,
- the volatility of the underlying
(
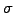 or Volatility) estimated as the
standard deviation of closing prices in
sect.1.5, e.g. 0.5 for 50 percent for a volatile share.
or Volatility) estimated as the
standard deviation of closing prices in
sect.1.5, e.g. 0.5 for 50 percent for a volatile share.
To clearly visualize the payoff dynamics from the Black-Scholes model,
it is useful to increase the interest rate and the dividend yield to
artificially large values and study with the VMARKET applet
below how the parameters affect the price of a
European call struck for 10 EUR six months before expiry.
VMARKET applet: press Start/Stop
to visualize the payoff dynamics of a European call.
The value of the option V(S,t) is plotted as a function of the
price of the underlying S, using un-realistically large
parameters to show the combined effect of a finite volatility,
interest rate and dividend yield. Switch from a Call to
Put option and observe carefully what happens.
|
|
"; ?>
The evolution of the payoff 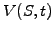 should be far from obvious, but can
be disentangled by investigating the effect of each parameter separately.
should be far from obvious, but can
be disentangled by investigating the effect of each parameter separately.
Have a look first at the volatility using the VMARKET applet above.
These experiments show that the main effect of the volatility is to
``smear out sharp edges'', i.e. where the vanilla call and put options
are at-the-money
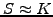 .
This phenomenon, known as diffusion in engineering sciences, is
strongest at the begining of the simulation when the option is close
to expiry date. It is the result of unpredictable market fluctuations:
even if the value of the underlying share is below the strike price of
a call
.
This phenomenon, known as diffusion in engineering sciences, is
strongest at the begining of the simulation when the option is close
to expiry date. It is the result of unpredictable market fluctuations:
even if the value of the underlying share is below the strike price of
a call 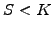 before the expiry date, there is a finite chance that the
market price will suddenly rise above that value, which would allow the
holder of a call option to make a final profit
before the expiry date, there is a finite chance that the
market price will suddenly rise above that value, which would allow the
holder of a call option to make a final profit
![$ \max[S(T)-K,0]$](s4img72.gif) .
Such a right to make a potential profit without any obligation has of
course a finite value, which decreases as the time approaches the
expiry date.
.
Such a right to make a potential profit without any obligation has of
course a finite value, which decreases as the time approaches the
expiry date.
Now play with the VMARKET applet below, using the default
parameters focusing on the effect of the interest rate.
VMARKET applet: press Start/Stop
to visualize the the effect of a finite interest rate (SpotRate)
and a dividend yield (Dividend) on the payoff dynamics of a
European put option V(S,t).
|
|
"; ?>
The effect of the risk-free interest rate can be understood from the
drift that affects any type of investment: to finally coincide with
the exercise price 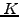 on the expiry date, the strike price has to be
discounted back in time (1.3#eq.6) to
on the expiry date, the strike price has to be
discounted back in time (1.3#eq.6) to
![$ K\times\exp[-r(T-t)]$](s4img75.gif) .
This is clearly visible in the applet, where the value at-the-money
shifts to lower prices as the simulation runs backward in time.
With a drift that is proportional to the strike price, the interest
rate appears to have its largest relative effect when the option is
at-the-money while the underlying is kept fixed; this is somewhat
misleading, since the underlying should also grow by the same amount
but is here used as a parameter.
In fact, the graph could be continuously renormalized with the same
amplification factor for the share, strike and option value-e.g.
introducing a new currency after every time step, so that the graph
would not evolve anymore at all.
.
This is clearly visible in the applet, where the value at-the-money
shifts to lower prices as the simulation runs backward in time.
With a drift that is proportional to the strike price, the interest
rate appears to have its largest relative effect when the option is
at-the-money while the underlying is kept fixed; this is somewhat
misleading, since the underlying should also grow by the same amount
but is here used as a parameter.
In fact, the graph could be continuously renormalized with the same
amplification factor for the share, strike and option value-e.g.
introducing a new currency after every time step, so that the graph
would not evolve anymore at all.
The following experiments can be carried out in the VMARKET
applet above.
Hopefully, these last experiments contribute more to your understanding
than your confusion: with payments that are proportional to the underlying,
the dividend yield continuously reduces the value of the share by the same
amount; this results in a drift along the horizontal axis (in the opposite
direction from the effect of interest rates) and appears as if the share
prices were amplified when the time runs backwards.
If the interest rate is equal to the dividend yield, the drifts in the
horizontal direction cancel out and all that remains is the effect from
the discounting at a risk-free interest rate.
With a good intuition for each parameter taken separately, it is a good
exercise to now return to the first applet
and discuss the main features that characterize an option payoff when
all the parameters are combined into one calculation.
Also, remember that unrealistically large parameters have been used in
this section to exaggerate the effect from each parameter; realistic
values will be used for an real option pricing calculation in the next
section.
SYLLABUS Previous: 4.1.1 The European Black-Scholes
Up: 4.1 Plain vanilla stock
Next: 4.1.3 Application, time value


 ','..','$myPermit') ?>
SYLLABUS Previous: 4.1.1 The European Black-Scholes
Up: 4.1 Plain vanilla stock
Next: 4.1.3 Application, time value
','..','$myPermit') ?>
SYLLABUS Previous: 4.1.1 The European Black-Scholes
Up: 4.1 Plain vanilla stock
Next: 4.1.3 Application, time value
![]() for a vanilla option or
StrikePrice in the applet) and the
numerical parameters that specify the
precision of the calculation (such as the TimeStep,
Walkers and MeshPoints), the Black-Scholes model depends
on only four financial parameters:
for a vanilla option or
StrikePrice in the applet) and the
numerical parameters that specify the
precision of the calculation (such as the TimeStep,
Walkers and MeshPoints), the Black-Scholes model depends
on only four financial parameters:
![]() .
This phenomenon, known as diffusion in engineering sciences, is
strongest at the begining of the simulation when the option is close
to expiry date. It is the result of unpredictable market fluctuations:
even if the value of the underlying share is below the strike price of
a call
.
This phenomenon, known as diffusion in engineering sciences, is
strongest at the begining of the simulation when the option is close
to expiry date. It is the result of unpredictable market fluctuations:
even if the value of the underlying share is below the strike price of
a call ![]() before the expiry date, there is a finite chance that the
market price will suddenly rise above that value, which would allow the
holder of a call option to make a final profit
before the expiry date, there is a finite chance that the
market price will suddenly rise above that value, which would allow the
holder of a call option to make a final profit
![]() .
Such a right to make a potential profit without any obligation has of
course a finite value, which decreases as the time approaches the
expiry date.
.
Such a right to make a potential profit without any obligation has of
course a finite value, which decreases as the time approaches the
expiry date.
![]() on the expiry date, the strike price has to be
discounted back in time (1.3#eq.6) to
on the expiry date, the strike price has to be
discounted back in time (1.3#eq.6) to
![]() .
This is clearly visible in the applet, where the value at-the-money
shifts to lower prices as the simulation runs backward in time.
With a drift that is proportional to the strike price, the interest
rate appears to have its largest relative effect when the option is
at-the-money while the underlying is kept fixed; this is somewhat
misleading, since the underlying should also grow by the same amount
but is here used as a parameter.
In fact, the graph could be continuously renormalized with the same
amplification factor for the share, strike and option value-e.g.
introducing a new currency after every time step, so that the graph
would not evolve anymore at all.
.
This is clearly visible in the applet, where the value at-the-money
shifts to lower prices as the simulation runs backward in time.
With a drift that is proportional to the strike price, the interest
rate appears to have its largest relative effect when the option is
at-the-money while the underlying is kept fixed; this is somewhat
misleading, since the underlying should also grow by the same amount
but is here used as a parameter.
In fact, the graph could be continuously renormalized with the same
amplification factor for the share, strike and option value-e.g.
introducing a new currency after every time step, so that the graph
would not evolve anymore at all.