

 SYLLABUS Previous: 4.3 Methods for European
Up: 4.3 Methods for European
Next: 4.3.2 Solution of the
SYLLABUS Previous: 4.3 Methods for European
Up: 4.3 Methods for European
Next: 4.3.2 Solution of the
4.3.1 Transformation to log-normal variables
[ SLIDE
transformation ||
VIDEO
modem -
LAN -
DSL]
The log-normal distribution of the price increments (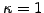 in
3.3.1#eq.1) chosen to derive the Black-Scholes equation (3.4#eq.4)
shows that the asset price
in
3.3.1#eq.1) chosen to derive the Black-Scholes equation (3.4#eq.4)
shows that the asset price 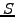 and the time
and the time 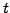 are in fact not a
natural choice of variables for the price of an option that expires
at a time
are in fact not a
natural choice of variables for the price of an option that expires
at a time 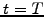 .
This motivates a transformation from financial variables
.
This motivates a transformation from financial variables 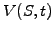 to log-normal variables
to log-normal variables 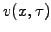 defined by
defined by
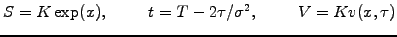 |
(4.3.1#eq.1) |
Substitute these in the Black-Scholes equation (be careful with the
second derivative)
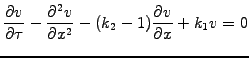 |
(4.3.1#eq.2) |
showing that only two dimensionless parameters in fact characterize the problem
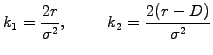 |
(4.3.1#eq.3) |
With a little more algebra, you can verify that further scaling by
![$\displaystyle V=Kv=K\exp\left[-\frac{1}{2}(k_2-1)x -\left(\frac{1}{4}(k_2-1)^2 +k_1\right)\tau\right] u(x,\tau)$](s4img85.gif) |
(4.3.1#eq.4) |
transforms Black-Scholes into a normalized diffusion equation
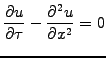 |
(4.3.1#eq.5) |
which bears a strong resemblance with the heat-equation from
engineering sciences.
This equation has to be solved for
![$ x \in [-\infty; \infty]$](s4img87.gif) ,
, 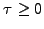 using boundary
using boundary
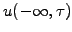 ,
,
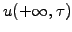 and initial
conditions
and initial
conditions 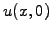 that have to be derived from no-arbitrage arguments
with financial variable
that have to be derived from no-arbitrage arguments
with financial variable 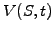 via the transformations (4.3.1#eq.1
and 4.3.1#eq.4).
.
via the transformations (4.3.1#eq.1
and 4.3.1#eq.4).
.
SYLLABUS Previous: 4.3 Methods for European
Up: 4.3 Methods for European
Next: 4.3.2 Solution of the


 SYLLABUS Previous: 4.3 Methods for European
Up: 4.3 Methods for European
Next: 4.3.2 Solution of the
SYLLABUS Previous: 4.3 Methods for European
Up: 4.3 Methods for European
Next: 4.3.2 Solution of the