

 ','..','$myPermit') ?>
SYLLABUS Previous: 5.1 Discound bonds
Up: 5.1 Discound bonds
Next: 5.1.2 Parameters illustrated with
','..','$myPermit') ?>
SYLLABUS Previous: 5.1 Discound bonds
Up: 5.1 Discound bonds
Next: 5.1.2 Parameters illustrated with
5.1.1 Term structure models for dummies
[ SLIDE
hedging -
experiments -
forecasting models ||
VIDEO
99) echo "
modem -
LAN -
DSL
"; else echo "login";?>
]
Imagine a portfolio with two identical discount bonds, except that
the first 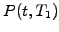 expires some time before the second
expires some time before the second 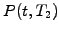 .
What is the effect of a market fluctuation, which suddenly rises the
spot rate at a time
.
What is the effect of a market fluctuation, which suddenly rises the
spot rate at a time 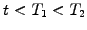 before the first bond reaches maturity?
The bonds are correlated and both will loose some of their original
value; since there is more time left for another fluctuation to step
back in the opposite direction, it is reasonable to assume that the
second bond with a longer time to maturity will be less affected.
before the first bond reaches maturity?
The bonds are correlated and both will loose some of their original
value; since there is more time left for another fluctuation to step
back in the opposite direction, it is reasonable to assume that the
second bond with a longer time to maturity will be less affected.
Taking advantage of this correlation, Vasicek creates a portfolio with a
positive holding in the first bond and a negative holding in the second.
By choosing exactly the right balance, this delta-hedging cancels out
the uncertain effect from fluctuations and leaves only a deterministic
change in the portfolio value. This is then used to calculate the fair
price of a bond.
The normalized value of the discount function is of course known at the
maturity 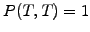 and the calculation is carried out with a forecast
of the interest rates backward in time to predict the fair value
and the calculation is carried out with a forecast
of the interest rates backward in time to predict the fair value
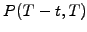 for an increasing lifetime
for an increasing lifetime 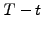 .
.
The VMARKET applet below illustrates the
procedure for a bond lifetime with up to RunTime=10 years.
VMARKET applet: press Start/Stop
to simulate the price of a zero-coupon bond backward in time, for a
market with a volatile spot rate paying a reward for the associated
risk.
The plots show the value of the discount function as a function of the
spot rate (P[r] in black) for an increasing time to maturity
t (Time on the top of the window, in years). Directly
derived from that using (2.2.2#eq.1),
two plots show the evolution of the yield curve (Y[r] in blue,
for a fixed Time) and the term structure of the interest rates
(Y[t] in grey, for a fixed SpotRate).
The latter acquires a finite value and sweeps across the plot window
over the time span of one simulation [0; RunTime] and is best
viewed after rescaling with Display.
|
|
"; ?>For a given value of the spot rate 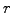 (horizontal axis, chosen to
reflect the current market conditions), the discount function
(horizontal axis, chosen to
reflect the current market conditions), the discount function 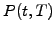 is decreasing backward in time
is decreasing backward in time 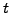 . Indeed, investors expect a return
from their investment, which shows up as a growth of the discount
function when the time runs forward so as to reach exactly one at
maturity. The reward can be measured using (2.2.2#eq.1) as a yield
. Indeed, investors expect a return
from their investment, which shows up as a growth of the discount
function when the time runs forward so as to reach exactly one at
maturity. The reward can be measured using (2.2.2#eq.1) as a yield
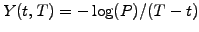 and differs from the spot rate
and differs from the spot rate 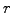 because of
the uncertain evolution of the future rates.
because of
the uncertain evolution of the future rates.
Due to the cyclic nature of the economy and the changes in the central
bank interest rates, economists generally forecast what may be the
future evolution of spot rates
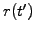 with
with
![$ t^\prime\in[t,T]$](s5img55.gif) .
This opinion consists of a drift (``the spot rate will fall'') and a
volatility (``the spot rate will fluctuate'') that can be estimated
from historical values (exercise 1.05).
.
This opinion consists of a drift (``the spot rate will fall'') and a
volatility (``the spot rate will fluctuate'') that can be estimated
from historical values (exercise 1.05).
";?>
Masters: one factor models to forecast the term structure of interest rates.
A broad class of models can already be obtained using only one driving
term for the uncertainty and assuming a normal distribution of the
interest rate increments of the form
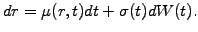 |
(5.1.1#eq.1) |
";?>
Contrary to stock options where
the drift scales out of the Black-Scholes equation
(3.4#eq.4), the interest rate drifts play a crucial role for the
evolution of bond prices. Using the excess return
dP/dt-rP=(-m+ls)dP/dr when the stochastic term is neglected in (3.5#eq.6), different
models have been proposed to forecast the evolution of the interest rates.
 The Vasicek model
The Vasicek model
- accounts for a long-term average rate and investors appetite for risk
![$\displaystyle \frac{dP}{dt}-rP = \left[a(b-r) +\lambda\sigma\right] \frac{\partial P}{\partial r}$](s5img57.gif) |
(5.1.1#eq.2) |
";?>
The first term is a mean reversion process, where the interest rate is
pulled back to the level b at a velocity a.
The second term is proportional to the market price of risk l
and measures the extra return per unit risk expected by the investors
(3.5#eq.9).
 The Ho and Lee model
The Ho and Lee model
- uses the instantaneous forward rate F(0,0,t)
from the market
![$\displaystyle \frac{dP}{dt}-rP =\left[\frac{\partial F(0,0,t)}{\partial t} +\sigma^2 t\right] \frac{\partial P}{\partial r}$](s5img58.gif) |
(5.1.1#eq.3) |
";?>
to forecast a drift based on today's expectations without ever saturating.
 The Hull an White model
The Hull an White model
- circumvents this problem with an evolution
![$\displaystyle \frac{dP}{dt}-rP =\left[\frac{\partial F(0,0,t)}{\partial t} +a\b...
...+\frac{\sigma^2}{2a}\big(1-\exp(-2at)\big)\right] \frac{\partial P}{\partial r}$](s5img59.gif) |
(5.1.1#eq.4) |
";?>
which reproduces the slope of the initial instantaneous forward rates from
Ho and Lee, and later revert back to the long-term average F(0,0,t) with a velocity a.
 The VMARKET model
The VMARKET model
- (c.f. Vasicek) uses a modulation of the market price of risk
![$\displaystyle \frac{dP}{dt}-rP = \big[a(b-r) +\lambda\sigma\cos(2n\pi t/T)\big] \frac{\partial P}{\partial r}$](s5img60.gif) |
(5.1.1#eq.5) |
";?>
to reproduce economic cycles and help you develop and intuition.
Analytical solutions can be found provided that the parameters remain
constant [11,19]. A numerical solution is however needed
to account for the volatility hump observed in the markets
(5.1.1#fig.1):
the volatility starts at zero (no uncertainty with bond prices today),
reaches a maximum and drops again to zero at maturity (the price equals
the face value):
![$\displaystyle \sigma(t)\simeq\sigma_\mathrm{max} \left[1.7\left((1-t/T)-(1-t/T)^6\right)\right].$](s5img61.gif) |
(5.1.1#eq.6) |
";?>
Figure 5.1.1#fig.1:
Volatility hump during the 10 years lifetime of a bond.
|
|
SYLLABUS Previous: 5.1 Discound bonds
Up: 5.1 Discound bonds
Next: 5.1.2 Parameters illustrated with


 ','..','$myPermit') ?>
SYLLABUS Previous: 5.1 Discound bonds
Up: 5.1 Discound bonds
Next: 5.1.2 Parameters illustrated with
','..','$myPermit') ?>
SYLLABUS Previous: 5.1 Discound bonds
Up: 5.1 Discound bonds
Next: 5.1.2 Parameters illustrated with
![]() expires some time before the second
expires some time before the second ![]() .
What is the effect of a market fluctuation, which suddenly rises the
spot rate at a time
.
What is the effect of a market fluctuation, which suddenly rises the
spot rate at a time ![]() before the first bond reaches maturity?
The bonds are correlated and both will loose some of their original
value; since there is more time left for another fluctuation to step
back in the opposite direction, it is reasonable to assume that the
second bond with a longer time to maturity will be less affected.
before the first bond reaches maturity?
The bonds are correlated and both will loose some of their original
value; since there is more time left for another fluctuation to step
back in the opposite direction, it is reasonable to assume that the
second bond with a longer time to maturity will be less affected.
![]() and the calculation is carried out with a forecast
of the interest rates backward in time to predict the fair value
and the calculation is carried out with a forecast
of the interest rates backward in time to predict the fair value
![]() for an increasing lifetime
for an increasing lifetime ![]() .
.
![]() with
with
![]() .
This opinion consists of a drift (``the spot rate will fall'') and a
volatility (``the spot rate will fluctuate'') that can be estimated
from historical values (exercise 1.05).
.
This opinion consists of a drift (``the spot rate will fall'') and a
volatility (``the spot rate will fluctuate'') that can be estimated
from historical values (exercise 1.05).