

 ','..','$myPermit') ?>
SYLLABUS Previous: 5.1.1 Term structure models
Up: 5.1 Discound bonds
Next: 5.2 Credit derivatives
','..','$myPermit') ?>
SYLLABUS Previous: 5.1.1 Term structure models
Up: 5.1 Discound bonds
Next: 5.2 Credit derivatives
5.1.2 Parameters illustrated with VMARKET experiments
[ SLIDE
parameters -
discounting -
price of risk -
drifts ||
VIDEO
99) echo "
modem -
LAN -
DSL
"; else echo "login";?>
]
Since the terminal value of the discount function at the maturity is
simply 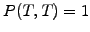 , the parameters characterize either the forecast of
the spot rate or the numerical method that will be examined later in
sect.5.3.1.
The financial parameters that are relevant in the applet are:
, the parameters characterize either the forecast of
the spot rate or the numerical method that will be examined later in
sect.5.3.1.
The financial parameters that are relevant in the applet are:
- the lifetime or maturity date (
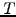 or
or RunTime)
of a bond in years, e.g. 10 for a bond reaching its maturity
in a decade,
- the maximum volatility (
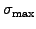 or
or
Volatility) of a bond estimated from historical values,
e.g. 0.02 for a two percent volatility peak that will be
reached after one third of the bond lifetime (5.1.1#fig.1),
- the market price of risk (
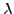 or
or MktPriceRsk)
measuring the reward
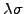 expected by the investors
for taking an investment risk, e.g. -0.25 in a risk averse market
with little appetite for risk.
In the applet, the effect is further modulated by a cosine
function reproducing (
expected by the investors
for taking an investment risk, e.g. -0.25 in a risk averse market
with little appetite for risk.
In the applet, the effect is further modulated by a cosine
function reproducing (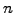 or
or UserDouble) economic cycles
during the lifetime of the bond,
- the mean reversion target rate (
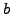 or
or MeanRevTarg)
is the value towards which the spot rate returns to after a long
time, e.g. 0.05 for a market with a 5% average rate,
- the mean reversion velocity (
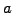 or
or MeanRevVelo)
measures the speed of the process, e.g. 0.5 [1/year] for a mean
reversion taking about 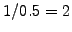 years.
years.
- the spot rate (
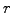 or
or SpotRate) used to plot the
term structure of the interest rates.
To visualize the evolution of a bond and the corresponding yield in a
very simple case, the VMARKET applet below
shows what happens in the absence of drifts (right hand side of
5.1.1#eq.5 equals zero) and without volatility.
VMARKET applet: press Start/Stop
to simulate the trivial case of a bond price, when the spot rate is
fixed to a pre-determined value.
The plots show the value of the discount function as a function of the
spot rate (P[r] in black) for an increasing time to maturity
t (Time on the top of the window, in years). Directly
derived from that using (2.2.1#eq.1),
two plots show the evolution of the yield curve (Y[r] in blue,
for a fixed Time) and the term structure of the interest rates
(Y[t] in grey, for a fixed SpotRate).
The latter acquires a finite value and sweeps across the plot window
over the time span of one simulation [0; RunTime] and is best
viewed after rescaling with Display.
|
|
"; ?>The discount function decreases exponentially backward in time
![$ P(t,T)=\exp(-r[T-t])$](s5img70.gif) as expected for a risk free investment
(1.3#eq.6).
The bond yield is equal to the spot rate
as expected for a risk free investment
(1.3#eq.6).
The bond yield is equal to the spot rate 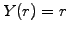 and the term structure
of the interest rates is constant
and the term structure
of the interest rates is constant 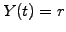 .
.
The second applet below illustrates the effect of
a large volatility 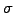 in the spot rate and accounts for the extra
return investors expect from the market through the so-called market
price of risk
in the spot rate and accounts for the extra
return investors expect from the market through the so-called market
price of risk 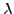 .
.
VMARKET applet: press Start/Stop
to study the effect of a large Volatility in the spot rate.
The extra reward payed in a risk averse market is here modeled
with the parameter MktPriceRsk.
The plots show the value of the discount function as a function of the
spot rate (P[r] in black) for an increasing time to maturity
t (Time on the top of the window, in years). Directly
derived from that using (2.2.1#eq.1),
two plots show the evolution of the yield curve (Y[r] in blue,
for a fixed Time) and the term structure of the interest rates
(Y[t] in grey, for a fixed SpotRate).
The latter acquires a finite value and sweeps across the plot window
over the time span of one simulation [0; RunTime] and is best
viewed after rescaling with Display.
|
|
"; ?>
Although this is not immediately apparent in the simulation, the main
effect of the volatility is to reduce the curvature of the discount
function 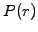 by smearing out irregularities in the yield curves
by smearing out irregularities in the yield curves
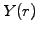 ,
, 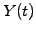 : if the forecast rate changes rapidly, the yield curves
do not follow immediately everywhere.
The reward payed to the investor who accepts the risk associated with
fluctuations in the spot rate is clearly visible, with an effective
yield that increases with time for a positive value of the market price
of risk
: if the forecast rate changes rapidly, the yield curves
do not follow immediately everywhere.
The reward payed to the investor who accepts the risk associated with
fluctuations in the spot rate is clearly visible, with an effective
yield that increases with time for a positive value of the market price
of risk 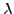 .
.
The applet above illustrates the effect of evolving
drifts in the forecast rates, here modeled with two economic cycles
during the lifetime of the bond: recession
 cut rate
cut rate
 over-heated economy
over-heated economy
 rise rate... or rather
the opposite when the time runs backward in the applet.
rise rate... or rather
the opposite when the time runs backward in the applet.
The third applet below finally illustrates the
effect of a mean reversion, which accounts for the tendency of the
forecasted rates to fall back to a long term average value.
VMARKET applet: press Start/Stop
to study the effect of a mean reversion process in the forecast
of interest rates. A target rate of 6 per cent (parameter
MeanRevTarg=0.06) is reached after approximatively 4 years
when choosing the inverse for MeanRevVelo=0.25.
The plots show the value of the discount function as a function of the
spot rate (P[r] in black) for an increasing time to maturity
t (Time on the top of the window, in years). Directly
derived from that using (2.2.1#eq.1),
two plots show the evolution of the yield curve (Y[r] in blue,
for a fixed Time) and the term structure of the interest rates
(Y[t] in grey, for a fixed SpotRate).
The latter acquires a finite value and sweeps across the plot window
over the time span of one simulation [0; RunTime] and is best
viewed after rescaling with Display.
|
|
"; ?>Observe how the yield rapidly drops for large values of the spot rate(on the right side of the plot), reflecting the reversion back to the long term average target.
Experimenting with the applet enables you to develop an intuitive
understanding for the fundamental processes that characterize the
credit market.
The experiments also prepare you also for the inverse problem, where
the term structure of the interest rates is known from the market
(e.g. 2.2.2#fig.1) and the drift / volatility parameters are matched
in order to extrapolate into the future (exercise 5.01).
SYLLABUS Previous: 5.1.1 Term structure models
Up: 5.1 Discound bonds
Next: 5.2 Credit derivatives


 ','..','$myPermit') ?>
SYLLABUS Previous: 5.1.1 Term structure models
Up: 5.1 Discound bonds
Next: 5.2 Credit derivatives
','..','$myPermit') ?>
SYLLABUS Previous: 5.1.1 Term structure models
Up: 5.1 Discound bonds
Next: 5.2 Credit derivatives
![]() , the parameters characterize either the forecast of
the spot rate or the numerical method that will be examined later in
sect.5.3.1.
The financial parameters that are relevant in the applet are:
, the parameters characterize either the forecast of
the spot rate or the numerical method that will be examined later in
sect.5.3.1.
The financial parameters that are relevant in the applet are:
![]() in the spot rate and accounts for the extra
return investors expect from the market through the so-called market
price of risk
in the spot rate and accounts for the extra
return investors expect from the market through the so-called market
price of risk ![]() .
.
![]() cut rate
cut rate
![]() over-heated economy
over-heated economy
![]() rise rate... or rather
the opposite when the time runs backward in the applet.
rise rate... or rather
the opposite when the time runs backward in the applet.