

 SYLLABUS Previous: 2.1.3 Plain vanilla options
Up: 2.1 The stock market
Next: 2.1.5 LEAPS and warrants
SYLLABUS Previous: 2.1.3 Plain vanilla options
Up: 2.1 The stock market
Next: 2.1.5 LEAPS and warrants
2.1.4 Exotic options
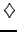
[ SLIDE
binary -
compound -
chooser -
barrier -
asian -
lookback ||
VIDEO
modem -
LAN -
DSL]
People generally refer to an exotic option
when the contract is not a plain vanilla put or call that are traded on an
open exchange and is instead traded over-the-counter (OTC).
 Binary or digital options
Binary or digital options
- may be the simplest form of exotic contracts: they only differ from the
vanilla options by the terminal payoff L(S)
that can be any positive function of the asset price S.
Some binaries can be obtained from the superposition of vanilla options:
straddles, bullish / bearish vertical spreads and
butterfly spreads are the subject of exercises 2.05-2.07.
Others have payoffs that remind well known functions, such as the
cash-or-nothing call reproducing the Heavyside H(x)
 |
(2.1.4#eq.1) |
and the supershare reminding the Dirac delta function
![$\displaystyle \Lambda_\mathrm{supershare} =\frac{1}{d}[\mathcal{H}(S-K) -\mathcal{H}(S-K-d)]$](s2img84.gif) |
(2.1.4#eq.2) |
with terminal payoff diagrams illustrated in (2.1.4#fig.1).
Figure 2.1.4#fig.1:
Example of binary / digital options with a general terminal payoff
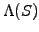 : a cash-or-nothing call (left) and a super-share (right).
: a cash-or-nothing call (left) and a super-share (right).
|
|
This generalization does not present any formal difficulty, but the
discontinuities in terminal payoff L(S)
do however seriously stretch the non-arbitrage arguments that will be
used to derive the Black-Scholes equation in chapter 3.
Indeed, a large amount of cash would be required to hedge small changes
in the price of the underlying as the option jumps from zero to a finite
value, only to fall back to zero shortly afterwards.
 Compound options
Compound options
- can be understood as options on options. In the simplest case, this
involves only put and call options and leads to four types compound
options. For example, the call-on-put carries the right at
time T1
to purchase for a price K1
a put option P2(K2,T2).
The coming chapters will show how to calculate the value of a put
option before it expires; denoting this as VP2(S,T1),
the payoff at expiry T1
gets
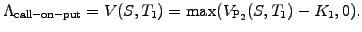 |
(2.1.4#eq.3) |
Since only one random variable governs the underlying asset price S and
its derivatives, the value of a compound option can be calculated by
solving first for the value of the option that may be bought or not, e.g. P2(K2,T2);
inserting this solution into (2.1.4#eq.3), the value of the compound
option is then obtained as usual.
 Chooser options
Chooser options
- are an extension of compound options, giving its holder the right at
time T1
to purchase for an amount K1
either a call C2(K2,T2) or
a put P2(K2,T2)
Going through all the possibilities, the same reasoning shows that at expiry T1
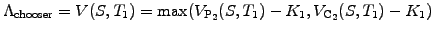 |
(2.1.4#eq.4) |
 Barrier options
Barrier options
- are characterized by a a condition set on the existence of the option.
When triggered, the right to exercise the option either appears
(in) or disappears (out) if the asset price is above
(up) or below (down) a prescribed barrier B:
- up-and-in options come into existence if S > B before expiry,
- up-and-out options cease to exist if S > B before expiry,
- down-and-in options come into existence if S < B before expiry,
- down-and-out options cease to exist if S < B before expiry.
Barrier options can be further complicated by making the knockout boundary
a function of time B(t) or by having a rebate if the barrier is activated.
In the latter case, the holder of the option receives a specified amount if
the barrier is reached.
 Asian options
Asian options
- have a payoff that depends on the price history of the underlying via some
kind of average.
Different definitions use a continuous S(t)
or a discrete sampling of the
price history {S(t1),S(t2)... S(tN)}
and involve an arithmetic
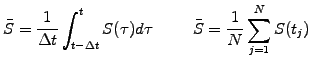 |
(2.1.4#eq.5) |
or geometric average
![$\displaystyle \bar{S}=\exp\left[\frac{1}{\Delta t}\int_{t-\Delta t}^{t} \log S(\tau)d\tau \right]\hspace{1cm} \bar{S}=\left[\prod_{j=1}^N S(t_j)\right]^{1/N}$](s2img90.gif) |
(2.1.4#eq.6) |
to define the strike price on the expiry date T.
An average strike call, for example, is structurally similar to
a vanilla call, with a payoff equal to the difference between the
asset price at expiry and its average if the difference is positive
and zero otherwise
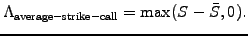 |
(2.1.4#eq.7) |
Such a product can be used to average out the price of an underlying
without the need for continuous re-hedging.
 Lookback options
Lookback options
- are similar in spirit as Asian options, except that the strike price
is a suitable definition of the maximum or minimum of the underlying
price history
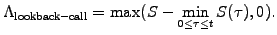 |
(2.1.4#eq.8) |
Such options can result in extremely advantageous payoffs and can therefore
be very expensive: think of an option that allows the holder to buy the
underlying at a low and sell it at a high.
 Russian options
Russian options
- are an example of perpetual options with an American exercise style:
at any time, Russian options pay out the maximum
realized asset price up to that date.
A variety of option can moreover be constructed by combining several
exotic features and the list presented here far from exhaustive.
SYLLABUS Previous: 2.1.3 Plain vanilla options
Up: 2.1 The stock market
Next: 2.1.5 LEAPS and warrants


 SYLLABUS Previous: 2.1.3 Plain vanilla options
Up: 2.1 The stock market
Next: 2.1.5 LEAPS and warrants
SYLLABUS Previous: 2.1.3 Plain vanilla options
Up: 2.1 The stock market
Next: 2.1.5 LEAPS and warrants
![\includegraphics[width=6cm]{figs/payCashNothing.eps}](s2img85.gif)
![\includegraphics[width=6cm]{figs/paySupershare.eps}](s2img86.gif)