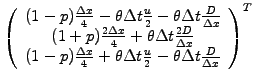 |
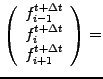 |
||
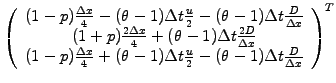 |
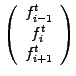 |
(1) |


 ','..','$myPermit') ?>
SYLLABUS Previous: 3.3 Numerical quadrature
Up: 3 FINITE ELEMENT METHOD
Next: 3.5 Linear solvers
','..','$myPermit') ?>
SYLLABUS Previous: 3.3 Numerical quadrature
Up: 3 FINITE ELEMENT METHOD
Next: 3.5 Linear solvers
Substituting the overlap integrals (3.3#eq.4) into (3.2#eq.5)
yields the FEM scheme
BandMatrix a = new BandMatrix(3, f.length);
BandMatrix b = new BandMatrix(3, f.length);
double[] c = new double[f.length];
double h = dx[0];
double htm = h*(1-tune)/4;
double htp = h*(1+tune)/4;
for (int j=0; j<=n; j++) {
a.setL(j, htm +h*(-0.5*beta -alpha)* theta );
a.setD(j,2*(htp +h*( alpha)* theta ));
a.setR(j, htm +h*( 0.5*beta -alpha)* theta );
b.setL(j, htm +h*(-0.5*beta -alpha)*(theta-1) );
b.setD(j,2*(htp +h*( alpha)*(theta-1)));
b.setR(j, htm +h*( 0.5*beta -alpha)*(theta-1) );
}
c=b.dot(f); //Right hand side
c[0]=c[0]+b.getL(0)*f[n]; // with periodicity
c[n]=c[n]+b.getR(n)*f[0];
fp=a.solve3(c); //Solve linear problem
Here again, the
BandMatrix.solve3()
method is used to compute a direct solution in
Having spent a considerable effort understanding the FEM formulation,
isn't it frustrating to see how similar the code is to the implicit
Crank-Nicholson FD scheme in sect.2.5?
This should be the main argument for the community who still uses
implicit finite difference schemes: with a little bit of thinking but
the same computational cost, the finite element scheme is now
considerably more flexibile: it is for example easy to densify the mesh16, modify the partly implicit time integration from centered to fully
implicit
![]() and tune the integration
and tune the integration ![]() .
Convince yourself that
Crank-Nicholson
(2.5.1#eq.12) and this
FEM scheme
(3.4#eq.1) are indeed equivalent when using a homogeneous mesh
.
Convince yourself that
Crank-Nicholson
(2.5.1#eq.12) and this
FEM scheme
(3.4#eq.1) are indeed equivalent when using a homogeneous mesh
![]() , a time centered integration
, a time centered integration
![]() and a trapezoidal quadrature
and a trapezoidal quadrature ![]() .
.
SYLLABUS Previous: 3.3 Numerical quadrature Up: 3 FINITE ELEMENT METHOD Next: 3.5 Linear solvers