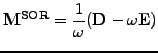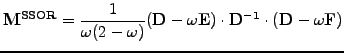','..','$myPermit') ?>
SYLLABUS Previous: 3.4 Implementation and solution
Up: 3 FINITE ELEMENT METHOD
Next: 3.6 Variational inequalities
','..','$myPermit') ?>
SYLLABUS Previous: 3.4 Implementation and solution
Up: 3 FINITE ELEMENT METHOD
Next: 3.6 Variational inequalities
3.5 Linear solvers
Slide : [ Direct
LU || Iterative
splitting :
Jacobi -
Gauss-Seidel -
SOR -
Preconditioning ||
VIDEO
99) echo "
modem -
ISDN -
LAN
"; else echo "login";?>
]
Writing efficient solvers for linear systems is a complete chapter of
numerical analysis and involves much more than what can be said in this
section. As a user of software libraries such as
Netlib
[5] or
PetSc
[3],
it is however sufficient to have only a rough idea of what type of
solvers exist and how to used them.
 Direct LU factorization.
Direct LU factorization.
- Remember that you should a never calculate a matrix inverse to solve
a linear system; the solution can be calculated with only one third
of the number of operations by decomposing the matrix into
Lower and Upper triangular parts [3.9] with
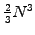 arithmetic operations
arithmetic operations 
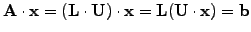 |
(1) |
and later use a forward and backward substitution of the
right hand side vector involving 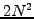 operations
operations
A particularly simple version has been implemented in JBONE for
tri-diagonal matrices, where the
solve3()
method computes the solution directly in
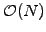 operations; the
first and the last equations are simply eliminated ``by hand'' to take
care of the periodicity.
Many different implementations of one and the same LU-factorization exist
taking advantage of the specific pattern of the matrix
operations; the
first and the last equations are simply eliminated ``by hand'' to take
care of the periodicity.
Many different implementations of one and the same LU-factorization exist
taking advantage of the specific pattern of the matrix
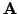 ; before
you start writing your own, check
Netlib
and it is likely that you
will find a routine tailored for your application.
; before
you start writing your own, check
Netlib
and it is likely that you
will find a routine tailored for your application.
When the matrix has more than three diagonals, it is important to allow for
a pivoting during the factorization process - interchanging rows and
columns in the matrix to avoid divisions by small numbers on the diagonal.
For particularly large problems, note the possibility of storing the matrix
on disk in a frontal implementation of the same algorithm.
When memory consumption, calculation time or parallelization become an
issue in 2, 3 or even higher dimensions, it might be useful to consider
iterative solvers as an alternative to the direct LU decomposition.
The idea behind them is best understood from a splitting of the
matrix into a sum17of a diagonal
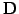 , strict lower
, strict lower
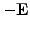 and upper
and upper
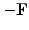 triangular parts
triangular parts
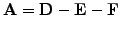 |
(3) |
An iterative solution of the problem
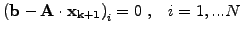 |
(4) |
is then sought where
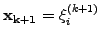 is the
is the 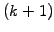 -th
approximation of the solution having components from
-th
approximation of the solution having components from 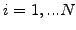 .
.
 Iterative Jacobi.
Iterative Jacobi.
- The simplest form of iteration consists in inverting only the diagonal
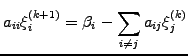 |
(5) |
which is equivalent in matrix notation to
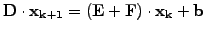 |
(6) |
Starting from an arbitrary initial guess
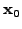 , simple
elliptic problems will -albeit slowly- converge to a stationary
point which is the solution of the linear problem.
, simple
elliptic problems will -albeit slowly- converge to a stationary
point which is the solution of the linear problem.
 Gauss-Seidel.
Gauss-Seidel.
- As the equations
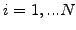 are updated one after the other, it is
possible to immediately use the updated components
are updated one after the other, it is
possible to immediately use the updated components
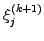 using forward Gauss-Seidel iterations
using forward Gauss-Seidel iterations
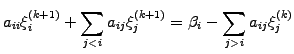 |
(7) |
or
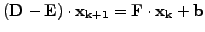 |
(8) |
where the calculation is carried out with the equation index increasing
from 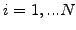 . The reverse is also possible and is called
backward Gauss-Seidel
. The reverse is also possible and is called
backward Gauss-Seidel
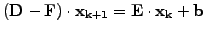 |
(9) |
 Successive over-relaxations - SOR
Successive over-relaxations - SOR
- are obtained when one of the Gauss-Seidel iterations (3.5#eq.8 or
3.5#eq.9) is linearly combined with the value of the previous step
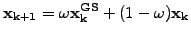 |
(10) |
using the parameter
![$ \omega\in[0;1]$](s3img135.gif) for an under-relaxation or
rather
for an under-relaxation or
rather
![$ \omega\in[1;2]$](s3img136.gif) for an over-relaxation.
A symmetric-SOR (SSOR) scheme is obtained with a combination
for an over-relaxation.
A symmetric-SOR (SSOR) scheme is obtained with a combination
![$\displaystyle \left\{\begin{array}{l}
(\mathbf{D} -\omega\mathbf{E})\cdot\mathb...
...a)\mathbf{D}\right]\cdot\mathbf{x_{k+1/2}}
+\omega\mathbf{b}
\end{array}\right.$](s3img137.gif) |
|
|
(11) |
 Preconditioning / approximate inverse.
Preconditioning / approximate inverse.
- Realizing that all the methods above are of the form
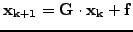 where
where
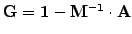 , the linear problem
can be diagonalized approximatively using a preconditioning
, the linear problem
can be diagonalized approximatively using a preconditioning
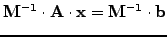 |
(12) |
where the preconditioner matrix
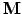 is one of
is one of
The product
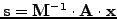 is calculated without ever forming the inverse, calculating first
is calculated without ever forming the inverse, calculating first
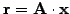 and then solving the linear
system
and then solving the linear
system
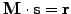 .
.
All these variants of Gauss-Seidel are simple and work fairly well for
reasonable sized (e.g.
 elliptic problems - making the
much more complicated multigrid approach attractive only for
large problems that have to be solved many times.
Hyperbolic (wave-) problems and non-Hermitian operators are more
difficult to solve iteratively and remains a matter of research
[18],[17].
Efficient methods in general rely on a suitable preconditioning
and the rapid convergence of Krylov or Lanczos methods, such as the
generalized minimal residuals (GMRES) and the
quasi-minimal residuals (QMR) [3.9].
elliptic problems - making the
much more complicated multigrid approach attractive only for
large problems that have to be solved many times.
Hyperbolic (wave-) problems and non-Hermitian operators are more
difficult to solve iteratively and remains a matter of research
[18],[17].
Efficient methods in general rely on a suitable preconditioning
and the rapid convergence of Krylov or Lanczos methods, such as the
generalized minimal residuals (GMRES) and the
quasi-minimal residuals (QMR) [3.9].
Note that the matrix-vector multiplications that are used to generate
new iterates can be performed in sparse format, i.e. using only
those matrix elements that are different from zero. This is the reason
why iterative methods can potentially be much more economical than
direct solvers - if they converge.
SYLLABUS Previous: 3.4 Implementation and solution
Up: 3 FINITE ELEMENT METHOD
Next: 3.6 Variational inequalities


 ','..','$myPermit') ?>
SYLLABUS Previous: 3.4 Implementation and solution
Up: 3 FINITE ELEMENT METHOD
Next: 3.6 Variational inequalities
','..','$myPermit') ?>
SYLLABUS Previous: 3.4 Implementation and solution
Up: 3 FINITE ELEMENT METHOD
Next: 3.6 Variational inequalities
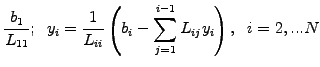
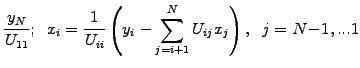
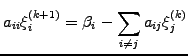
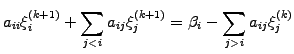
![$\displaystyle \left\{\begin{array}{l}
(\mathbf{D} -\omega\mathbf{E})\cdot\mathb...
...a)\mathbf{D}\right]\cdot\mathbf{x_{k+1/2}}
+\omega\mathbf{b}
\end{array}\right.$](s3img137.gif)