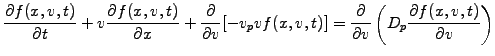','..','$myPermit') ?>
SYLLABUS Previous: 10.1 Interactive evaluation form
Up: 10 COURSE EVALUATION AND
Next: Bibliograpy
','..','$myPermit') ?>
SYLLABUS Previous: 10.1 Interactive evaluation form
Up: 10 COURSE EVALUATION AND
Next: Bibliograpy
10.2 Suggestions for one-week projects
The best ideas for a small one-week project stems directly from your own
field; please submit a short description to the course leader and don't
overestimate the work you can achieve during a week!
For those who need some suggestions, here are a number of projects listed
more or less in rising order of difficulty.
 Diffusion in an inhomogeneous medium.
Diffusion in an inhomogeneous medium.
- Let the advection
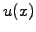 and diffusion coefficients
and diffusion coefficients 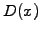 vary in space,
and solve the inhomogeneous advection-diffusion equation (1.3.2#eq.2)
with finite elements. Using a Gaussian quadrature instead of the analytical
calulation of the inner products (3.3#eq.4).
vary in space,
and solve the inhomogeneous advection-diffusion equation (1.3.2#eq.2)
with finite elements. Using a Gaussian quadrature instead of the analytical
calulation of the inner products (3.3#eq.4).
 Inhomogeneous mesh for diffusion with FEM.
Inhomogeneous mesh for diffusion with FEM.
- Add the capability of refining the mesh using the finite elements method.
Integrate analytically a sum of Lorentzian functions
![$ L_{[x_j,w_j]}(x)=w_j\left[w_j^2 +(x-x_j)^2\right]^{-2}$](s10img10.gif) defining the locations
defining the locations 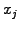 and the weights
and the weights 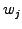 of the regions you want
to refine; this leads to an expression for the inhomogeneous distribution
of mesh points
of the regions you want
to refine; this leads to an expression for the inhomogeneous distribution
of mesh points
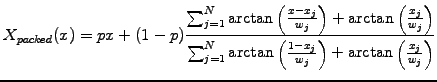 |
(1) |
Study the numerical convergence of a diffusion dominated problem in a
strongly inhomogeneous medium.
 The uncertain future of a predator-prey system.
The uncertain future of a predator-prey system.
- During uncertain (stochastic) feeding conditions, the Volterra-Lotka
system of equations (exercise 1.02) could be replaced by a stochastic
differential equation describing an ensemble of possible outcomes.
Study the evolution of the density distribution of the possible
population using a Monte Carlo method; check the possibility of an
extinction simply by ``bad luck''. Show that your solution converges
for small time steps.
 Wave equation as a driven problem.
Wave equation as a driven problem.
- Implement a computational scheme to solve the equation describing forced
oscillation in a weakly absorbing and bounded medium
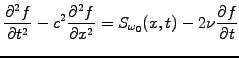 |
(2) |
Choose a source
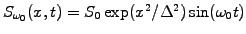 smoothly distributed inside the cavity
smoothly distributed inside the cavity
![$ x\in[-L/2;L/2]$](s10img16.gif) and a sink
and a sink
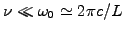 that is sufficiently small to allow
the perturbations to propagate and reflect.
Vary the driving frequency
that is sufficiently small to allow
the perturbations to propagate and reflect.
Vary the driving frequency 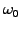 and study the possibility of
exciting resonances inside the cavity.
and study the possibility of
exciting resonances inside the cavity.
 Particle weight.
Particle weight.
- Apply individual weights
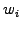 to the particles in the Monte Carlo
solver. Try to reduce the amount of noise at low levels in a steady
state solution (e.g. exercise 5.04) by splitting particles with
to the particles in the Monte Carlo
solver. Try to reduce the amount of noise at low levels in a steady
state solution (e.g. exercise 5.04) by splitting particles with
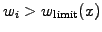 . Try to find a good maximum weight function
. Try to find a good maximum weight function
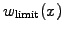 . After a while some particles will be to heavy.
Solve this by re-discretizing the distribution with
. After a while some particles will be to heavy.
Solve this by re-discretizing the distribution with
discretize(new ShapeNumerical(this)).
The particle weight should be used to increase the accuracy in
discretization. To complete this project, you will have to change
the projection, the discretization and learn the Java Vector
class.
 Option pricing.
Option pricing.
- Having implemented the FD and FEM schemes for the price
of European and American options (exercises 2.05 and 3.07), complete this
project implementing a MC solver for a
out-barrier option,
which looses all its value when the underlying exceeds a certain value.
Validate each scheme with comparisons in the parameter range where all
three overlap.
 Bose-Einstein condensation.
Bose-Einstein condensation.
- Start with the linear Schrödinger equation
![$\displaystyle i\frac{\partial \psi}{\partial t} = \left[ -\frac{\partial^2}{\partial x^2} + V(x) \right] \psi$](s10img22.gif) |
(3) |
normalized with Plank's constant 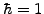 and a particle mass
and a particle mass 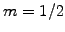 and use two different schemes to calculate the scattering of a wavepacket
by a simple one-dimensional potential
and use two different schemes to calculate the scattering of a wavepacket
by a simple one-dimensional potential 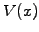 .
Having validated your schemes with analytical results, solve the non-linear
equation describing the Bose-Einstein condensation in a parabolic trapping
potential
.
Having validated your schemes with analytical results, solve the non-linear
equation describing the Bose-Einstein condensation in a parabolic trapping
potential
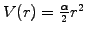 with cylindrical symmetry
with cylindrical symmetry
![$\displaystyle i\frac{\partial \psi}{\partial t} = \left[ -\frac{1}{r}\frac{\par...
...\frac{\partial }{\partial r}\right) + V(r) + 2\pi a \mid\psi\mid^2 \right] \psi$](s10img27.gif) |
(4) |
where the parameter 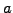 defines the scattering length.
defines the scattering length.
 Slowing down of beams.
Slowing down of beams.
- The slowing down of a beam in a collisional medium is given by
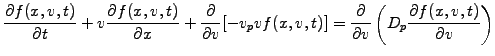 |
(5) |
Use Monte Carlo for solving the beam distribution
function. Identify the drift and diffusion coefficients in 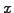 and
and 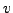 . Start the pulse to the left with
. Start the pulse to the left with 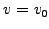 . Modify
. Modify 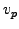 and
and 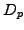 in order to get a nice slowing down of the pulse.
in order to get a nice slowing down of the pulse.
SYLLABUS Previous: 10.1 Interactive evaluation form
Up: 10 COURSE EVALUATION AND
Next: Bibliograpy


 ','..','$myPermit') ?>
SYLLABUS Previous: 10.1 Interactive evaluation form
Up: 10 COURSE EVALUATION AND
Next: Bibliograpy
','..','$myPermit') ?>
SYLLABUS Previous: 10.1 Interactive evaluation form
Up: 10 COURSE EVALUATION AND
Next: Bibliograpy