

 ','..','$myPermit') ?>
SYLLABUS Previous: 1.3.3 Dispersion
Up: 1.3 Prototype problems
Next: 1.3.5 Schrödinger
','..','$myPermit') ?>
SYLLABUS Previous: 1.3.3 Dispersion
Up: 1.3 Prototype problems
Next: 1.3.5 Schrödinger
1.3.4 Wave-breaking
Slide : [
wave-breaking -
shock-waves -
solitons ||
VIDEO
99) echo "
modem -
ISDN -
LAN
"; else echo "login";?>
]
Wave-breaking is a non-linearity that is particularly nicely
understood when surfing on a see shore, where shallow waters steepen
the waves until they break. The process can be modeled theoretically
from the advection equation by choosing the
velocity proportional to the amplitude 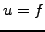 :
:
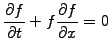 |
(1.3.4#eq.1) |
Since a local maximum (large 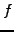 ) propagates faster than a local minimum
(small
) propagates faster than a local minimum
(small 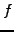 ), the top of the wave tries to over-take the bottom.
The function soon becomes multi-valued causing the wave (and our numerical
schemes) to break.
Sometimes, the wave-breaking is balanced by a competing mechanism.
This is the case of example in the Burger equation for
shock-waves
), the top of the wave tries to over-take the bottom.
The function soon becomes multi-valued causing the wave (and our numerical
schemes) to break.
Sometimes, the wave-breaking is balanced by a competing mechanism.
This is the case of example in the Burger equation for
shock-waves
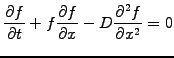 |
(1.3.4#eq.2) |
where the creation of a shock front (with short wavelengths) is physically
limited by diffusion, which damps the short wavelengths (1.3.2#eq.4).
Here is an example of
a shock formation computed using a 2-levels explicit finite difference
scheme from chapter 2.
JBONE applet: press Start/Stop
to simulate the propagation of a shock front using the Burger equation,
where the wave-breaking non-linearity is balanced by a finite diffusion.
|
|
"; ?>
Another type of non-linear equations where the wave-breaking is balanced by
dispersion leads to the Korteweg-DeVries equation for solitons
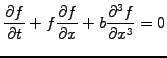 |
(1.3.4#eq.3) |
The evolution below
shows how large amplitudes solitons (short wavelengths) propagate
faster than lower amplitudes (long wavelength), in agreement with the
dispersion analysis previously performed in
sect.1.3.3.
JBONE applet: press Start/Stop
to simulate the propagation of solitons using the KdV equation,
where the wave-breaking non-linearity is balanced by a finite
dispersion.
|
|
"; ?>
SYLLABUS Previous: 1.3.3 Dispersion
Up: 1.3 Prototype problems
Next: 1.3.5 Schrödinger


 ','..','$myPermit') ?>
SYLLABUS Previous: 1.3.3 Dispersion
Up: 1.3 Prototype problems
Next: 1.3.5 Schrödinger
','..','$myPermit') ?>
SYLLABUS Previous: 1.3.3 Dispersion
Up: 1.3 Prototype problems
Next: 1.3.5 Schrödinger
![]() :
: