

 ','..','$myPermit') ?>
SYLLABUS Previous: 1.3.4 Wave-breaking
Up: 1.3 Prototype problems
Next: 1.4 Numerical discretization
','..','$myPermit') ?>
SYLLABUS Previous: 1.3.4 Wave-breaking
Up: 1.3 Prototype problems
Next: 1.4 Numerical discretization
1.3.5 Schrödinger
Slide : [
Schrödinger ||
VIDEO
99) echo "
modem -
ISDN -
LAN
"; else echo "login";?>
]
Choosing units where Planck's constant 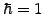 and the mass
and the mass 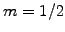 ,
the time-dependent Schrödinger equation clearly appears as a
special type of wave / diffusion equation:
,
the time-dependent Schrödinger equation clearly appears as a
special type of wave / diffusion equation:
In quantum mechanics, the Schrödinger equation is used to evolve the
complex wave-function
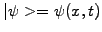 to describe the probability
to describe the probability
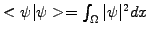 of finding a particle in a
given interval
of finding a particle in a
given interval
![$ \Omega=[x_L;x_R]$](s1img117.gif) .
Take the simplest example of a free particle modeled with a wave-packet
in a periodic domain and assume a constant potential
.
Take the simplest example of a free particle modeled with a wave-packet
in a periodic domain and assume a constant potential 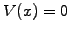 .
The JBONE applet below shows the evolution
of a low energy
.
The JBONE applet below shows the evolution
of a low energy
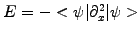 (long wavelength) particle
that is initially known with a rather good accuracy in space (narrow
Gaussian envelope):
(long wavelength) particle
that is initially known with a rather good accuracy in space (narrow
Gaussian envelope):
JBONE applet: press Start/Stop
to run the simulation showing how a well localized low energy
wave-packet spreads out in time, in agreement with Heisenberg's
uncertainty principle in quantum mechanics.
|
|
"; ?>
the wave-function
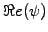 (blue line) starts to oscillate, the
probability density
(blue line) starts to oscillate, the
probability density 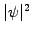 spreads out (black line) and the position
increasingly becomes uncertain... reproducing the famous uncertainty
principle.
spreads out (black line) and the position
increasingly becomes uncertain... reproducing the famous uncertainty
principle.
SYLLABUS Previous: 1.3.4 Wave-breaking
Up: 1.3 Prototype problems
Next: 1.4 Numerical discretization


 ','..','$myPermit') ?>
SYLLABUS Previous: 1.3.4 Wave-breaking
Up: 1.3 Prototype problems
Next: 1.4 Numerical discretization
','..','$myPermit') ?>
SYLLABUS Previous: 1.3.4 Wave-breaking
Up: 1.3 Prototype problems
Next: 1.4 Numerical discretization
![]() and the mass
and the mass ![]() ,
the time-dependent Schrödinger equation clearly appears as a
special type of wave / diffusion equation:
,
the time-dependent Schrödinger equation clearly appears as a
special type of wave / diffusion equation: