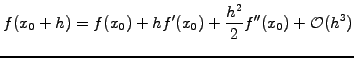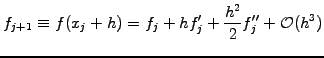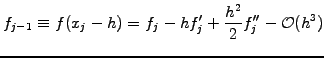','..','$myPermit') ?>
SYLLABUS Previous: 1.4.1 Convergence, Richardson extrapolation
Up: 1.4 Numerical discretization
Next: 1.4.3 Finite elements
','..','$myPermit') ?>
SYLLABUS Previous: 1.4.1 Convergence, Richardson extrapolation
Up: 1.4 Numerical discretization
Next: 1.4.3 Finite elements
1.4.2 Sampling on a regular grid
The main advantage of sampling data on a grid is its simplicity:
starting from a continuous function 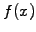 a finite number of values
a finite number of values
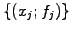 are measured on what is generally a homogeneous mesh
are measured on what is generally a homogeneous mesh
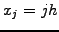 ,
, 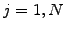 .
The values at the domain boundary appear explicitly as
.
The values at the domain boundary appear explicitly as 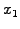 and
and 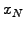 .
.
Figure:
Approximation of 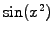 on a homogeneous mesh.
on a homogeneous mesh.
|
|
Figure (1.4.2#fig.1) shows that the sampled function is unknown almost
everywhere, except on the grid points where it is exact.
If the sampling is dense enough and the function smooth, intermediate
values can be interpolated from neighboring data using a Taylor expansion
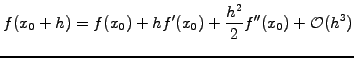 |
(1.4.2#eq.1) |
Combining Taylor expansions from the same function evaluated on
neighboring locations 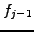 ,
, 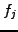 ,
, 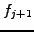 ,
, 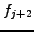 , etc.
For example, the difference
, etc.
For example, the difference
leads to the finite difference approximations that has previously been used
in sect.1.2.1. Along the same lines, you can derive the formula
for the k-th derivative 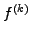 from Abramowitz [1] §25.1.2
from Abramowitz [1] §25.1.2
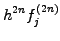 |
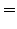 |
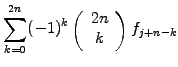 |
(1.4.2#eq.2) |
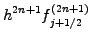 |
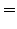 |
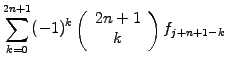 |
(1.4.2#eq.3) |
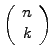 |
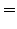 |
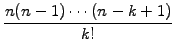 |
|
Remember that a discretization on a grid is non-compact: the convergence
depends not only on the initial discretization, but also on the
interpolation that is required afterwards to reconstruct the data between
the mesh points.
SYLLABUS Previous: 1.4.1 Convergence, Richardson extrapolation
Up: 1.4 Numerical discretization
Next: 1.4.3 Finite elements


 ','..','$myPermit') ?>
SYLLABUS Previous: 1.4.1 Convergence, Richardson extrapolation
Up: 1.4 Numerical discretization
Next: 1.4.3 Finite elements
','..','$myPermit') ?>
SYLLABUS Previous: 1.4.1 Convergence, Richardson extrapolation
Up: 1.4 Numerical discretization
Next: 1.4.3 Finite elements
![]() a finite number of values
a finite number of values
![]() are measured on what is generally a homogeneous mesh
are measured on what is generally a homogeneous mesh
![]() ,
, ![]() .
The values at the domain boundary appear explicitly as
.
The values at the domain boundary appear explicitly as ![]() and
and ![]() .
.