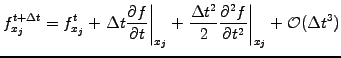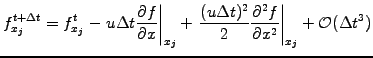','..','$myPermit') ?>
SYLLABUS Previous: 2.2 Explicit 3 levels
Up: 2 FINITE DIFFERENCES
Next: 2.4 Leap-frog, staggered grids
','..','$myPermit') ?>
SYLLABUS Previous: 2.2 Explicit 3 levels
Up: 2 FINITE DIFFERENCES
Next: 2.4 Leap-frog, staggered grids
2.3 Lax-Wendroff
Slide : [ Lax-Wendroff
Scheme -
Code -
Run ||
VIDEO
99) echo "
modem -
ISDN -
LAN
"; else echo "login";?>
]
Rather than counting on your intuition for the right combination of terms,
is it possible to formulate a systematic recipe for solving an equation in
Eulerian coordinates and with any chosen level of accuracy?
Yes, using the so-called Lax-Wendroff approach, which can easily be
generalized for non-linear and vector equations.
- Discretize the function on a regular grid
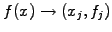 ,
, 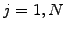 ,
,
- Expand the differential operators in time using a Taylor series
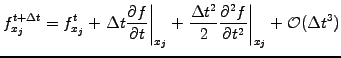 |
(2.3.0#eq.6) |
- Substitute the time derivatives from the master equation;
for the case of advection (1.3.1#eq.1), this yields
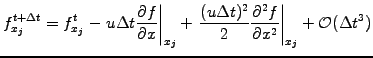 |
(2.3.0#eq.7) |
- Use centered differences for spatial operators
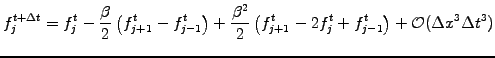 |
(2.3.0#eq.8) |
The example here yields a
second order Lax-Wendroff scheme
for advection that is explicit, centered and stable provided that
the CFL number
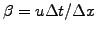 remains below unity:
remains below unity:
for (int j=1; j<n; j++) {
fp[j]=f[j] -0.5*beta *(f[j+1]-f[j-1])
+0.5*beta*beta*(f[j+1]-2.*f[j]+f[j-1]); }
fp[0]=f[0] -0.5*beta *(f[ 1 ]-f[ n ])
+0.5*beta*beta*(f[ 1 ]-2.*f[0]+f[ n ]);
fp[n]=f[n] -0.5*beta *(f[ 0 ]-f[n-1])
+0.5*beta*beta*(f[ 0 ]-2.*f[n]+f[n-1]);
JBONE applet: press Start/Stop
to simulate the advection of a box function and to test how the
second order explicit Lax-Wendroff scheme affects the dispersion and
the damping of short and long wavelengths superposed in a box function.
|
|
"; ?>
The JBONE applet below illustrates how
the Lax-Wendroff scheme combines the properties of the 2 and 3 levels
schemes from the two previous sections.
SYLLABUS Previous: 2.2 Explicit 3 levels
Up: 2 FINITE DIFFERENCES
Next: 2.4 Leap-frog, staggered grids
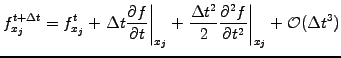
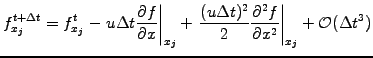


 ','..','$myPermit') ?>
SYLLABUS Previous: 2.2 Explicit 3 levels
Up: 2 FINITE DIFFERENCES
Next: 2.4 Leap-frog, staggered grids
','..','$myPermit') ?>
SYLLABUS Previous: 2.2 Explicit 3 levels
Up: 2 FINITE DIFFERENCES
Next: 2.4 Leap-frog, staggered grids