

 ','..','$myPermit') ?>
SYLLABUS Previous: 3.1 Mathematical background
Up: 3 FINITE ELEMENT METHOD
Next: 3.3 Numerical quadrature
','..','$myPermit') ?>
SYLLABUS Previous: 3.1 Mathematical background
Up: 3 FINITE ELEMENT METHOD
Next: 3.3 Numerical quadrature
3.2 An engineer's formulation
Slide : [
Weak form -
By parts -
time -
space -
Ax=b ||
VIDEO
99) echo "
modem -
ISDN -
LAN
"; else echo "login";?>
]
After a section on what a physicist believes is a mathematician's view
of the subject, it is time for an example. Using the format of a ``recipe''
that is applicable to a broad class of practical problems, we show here
how the advection-diffusion equation (1.3.2#eq.2) is discretized
using Galerkin linear finite elements (FEMs) and how it
is implemented.
 Derive a weak variational form.
Derive a weak variational form.
- ``Multiply'' your equation by
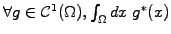 where the
complex conjugate is necessary only if your equation(s) is (are) complex
where the
complex conjugate is necessary only if your equation(s) is (are) complex
![$\displaystyle \forall g\in \mathcal{C}^1(\Omega),\hspace{1cm} \int_{x_L}^{x_R} ...
...+u\frac{\partial f}{\partial x} -D\frac{\partial^2 f}{\partial x^2} \right] = 0$](s3img38.gif) |
(1) |
 Integrate by parts,
Integrate by parts,
- so as to avoid having to use quadratic basis functions to discretize the
second order diffusion operator
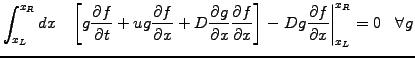 |
(2) |
Assuming a periodic domain, the surface term has here been canceled,
imposing natural boundary conditions.
 Discretize time
Discretize time
- with a finite difference backward in time and using a partially implicit
evaluation of the unknown
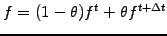 where
where
![$ \theta\in[1/2;1]$](s3img41.gif)
![$\displaystyle \int_{x_L}^{x_R}\!\!dx \left[ \frac{g}{\Delta t} +\theta ug\frac{...
...!\theta) D \frac{\partial g}{\partial x}\frac{\partial}{\partial x} \right] f^t$](s3img43.gif) |
(3) |
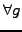 . All the unknowns have been reassembled on the left.
Re-scale by
. All the unknowns have been reassembled on the left.
Re-scale by 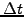 , and
, and
 Discretize space
Discretize space
- using linear roof-tops and a
Galerkin choice for the test functions
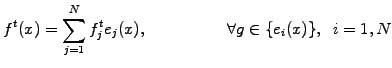 |
(4) |
Note how the condition
![$ \forall g\in \mathcal{C}^1([x_L; x_R])$](s3img52.gif) is here
used to create as many independent equations
is here
used to create as many independent equations 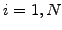 as there are unknowns
as there are unknowns
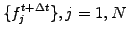 .
All the essential boundary conditions are then imposed by allowing
.
All the essential boundary conditions are then imposed by allowing
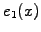 and
and 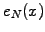 to overlap in the periodic domain.
Since only the basis and test functions
to overlap in the periodic domain.
Since only the basis and test functions
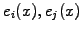 and perhaps the
problem coefficients
and perhaps the
problem coefficients
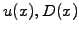 remain space dependent, the discretized
equations are all written in terms of inner products, involving
overlap integrals of the form
remain space dependent, the discretized
equations are all written in terms of inner products, involving
overlap integrals of the form
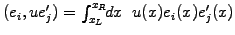 .
Reassembling them all in a matrix,
.
Reassembling them all in a matrix,
 Write a linear system
Write a linear system
- through which the unknown values from the next time step
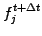 can implicitly be obtained from the current values
can implicitly be obtained from the current values 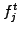 by solving a
linear system
by solving a
linear system
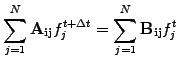 |
(6) |
To relate the Galerkin linear FEM scheme (3.2#eq.5) with the code
that has been implemented in the JBONE applet, it is necessary
now to evaluate the overlap integrals.
This is usually performed numerically using a quadrature. In the case of
a homogeneous mesh
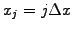 , a constant advection
, a constant advection 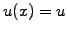 and
diffusion coefficient
and
diffusion coefficient 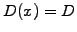 , the coming section shows how explicit
expressions can be obtained from the same rules to define directly the
matrix elements.
, the coming section shows how explicit
expressions can be obtained from the same rules to define directly the
matrix elements.
SYLLABUS Previous: 3.1 Mathematical background
Up: 3 FINITE ELEMENT METHOD
Next: 3.3 Numerical quadrature
![$\displaystyle \forall g\in \mathcal{C}^1(\Omega),\hspace{1cm} \int_{x_L}^{x_R} ...
...+u\frac{\partial f}{\partial x} -D\frac{\partial^2 f}{\partial x^2} \right] = 0$](s3img38.gif)
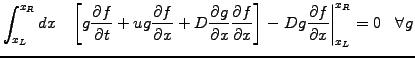
![$\displaystyle \int_{x_L}^{x_R} dx \left[ g\left(\frac{f^{t+\Delta t}-f^t}{\Delt...
...ial}{\partial x} \left[(1-\theta)f^t + \theta f^{t+\Delta t}\right] \right] = 0$](s3img42.gif)
![$\displaystyle \int_{x_L}^{x_R}\!\!dx \left[ \frac{g}{\Delta t} +\theta ug\frac{...
...!\theta) D \frac{\partial g}{\partial x}\frac{\partial}{\partial x} \right] f^t$](s3img43.gif)
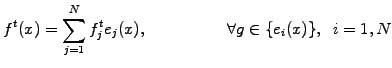


 ','..','$myPermit') ?>
SYLLABUS Previous: 3.1 Mathematical background
Up: 3 FINITE ELEMENT METHOD
Next: 3.3 Numerical quadrature
','..','$myPermit') ?>
SYLLABUS Previous: 3.1 Mathematical background
Up: 3 FINITE ELEMENT METHOD
Next: 3.3 Numerical quadrature
![$\displaystyle \forall g\in \mathcal{C}^1(\Omega),\hspace{1cm} \int_{x_L}^{x_R} ...
...+u\frac{\partial f}{\partial x} -D\frac{\partial^2 f}{\partial x^2} \right] = 0$](s3img38.gif)
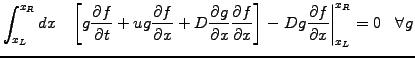
![$\displaystyle \int_{x_L}^{x_R} dx \left[ g\left(\frac{f^{t+\Delta t}-f^t}{\Delt...
...ial}{\partial x} \left[(1-\theta)f^t + \theta f^{t+\Delta t}\right] \right] = 0$](s3img42.gif)
![$\displaystyle \int_{x_L}^{x_R}\!\!dx \left[ \frac{g}{\Delta t} +\theta ug\frac{...
...!\theta) D \frac{\partial g}{\partial x}\frac{\partial}{\partial x} \right] f^t$](s3img43.gif)
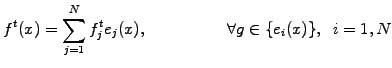
![]() , a constant advection
, a constant advection ![]() and
diffusion coefficient
and
diffusion coefficient ![]() , the coming section shows how explicit
expressions can be obtained from the same rules to define directly the
matrix elements.
, the coming section shows how explicit
expressions can be obtained from the same rules to define directly the
matrix elements.