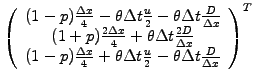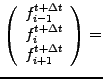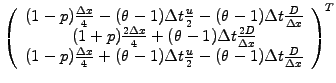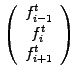3.4 Implementation and solution

','..','$myPermit') ?> SYLLABUS Previous: 3.3 Numerical quadrature Up: 3 FINITE ELEMENT METHOD Next: 3.5 Linear solvers

3.4 Implementation and solution

Slide : [ Scheme - Code - Run || VIDEO 99) echo " modem - ISDN - LAN "; else echo "login";?> ]

Substituting the overlap integrals (3.3#eq.4) into (3.2#eq.5) yields the FEM scheme

$\displaystyle \left(\begin{array}{c} (1-p)\frac{\Delta x}{4} -\theta\Delta t\fr... ...theta\Delta t\frac{u}{2} -\theta\Delta t\frac{D}{\Delta x} \end{array}\right)^T$	$\displaystyle \cdot$	$\displaystyle \left(\begin{array}{c} f_{i-1}^{t+\Delta t} \\ f_{i }^{t+\Delta t} \\ f_{i+1}^{t+\Delta t} \end{array}\right) =$
$\displaystyle \left(\begin{array}{c} (1-p)\frac{\Delta x}{4} -(\theta-1)\Delta ... ...)\Delta t\frac{u}{2} -(\theta-1)\Delta t\frac{D}{\Delta x} \end{array}\right)^T$	$\displaystyle \cdot$	$\displaystyle \left(\begin{array}{c} f_{i-1}^{t} \\ f_{i }^{t} \\ f_{i+1}^{t} \end{array}\right)$	(1)

Following an initialization where the initial condition is discretized with trivial projection on piecewise linear roof-top functions, the advection-diffusion scheme is implemented as

      BandMatrix a = new BandMatrix(3, f.length);
      BandMatrix b = new BandMatrix(3, f.length);
      double[]   c = new double[f.length];
      double h   = dx[0];
      double htm = h*(1-tune)/4;
      double htp = h*(1+tune)/4;

      for (int j=0; j<=n; j++) {
        a.setL(j,   htm +h*(-0.5*beta -alpha)* theta    );
        a.setD(j,2*(htp +h*(           alpha)* theta   ));
        a.setR(j,   htm +h*( 0.5*beta -alpha)* theta    );
        b.setL(j,   htm +h*(-0.5*beta -alpha)*(theta-1) );
        b.setD(j,2*(htp +h*(           alpha)*(theta-1)));
        b.setR(j,   htm +h*( 0.5*beta -alpha)*(theta-1) );
      }
      c=b.dot(f);                                 //Right hand side
      c[0]=c[0]+b.getL(0)*f[n];                   // with periodicity
      c[n]=c[n]+b.getR(n)*f[0];

      fp=a.solve3(c);                             //Solve linear problem

Here again, the BandMatrix.solve3() method is used to compute a direct solution in $\mathcal{O}(N)$ operations, using an LU-factorization that will be examined with more details in the coming section. The entire scheme is illustrated below with the advection of a box function, calculated using a piecewise linear FEM discretization (with

) and a partly implicit time integration (with $\theta=0.55$ ).

**JBONE applet:** press **Start/Stop** to simulate the advection of a box function, so as to test how the linear finite elements scheme affects the dispersion and the damping of short and long wavelengths superposed in a box function.
"; if ($user_nbr<100) echo " "; echo "

"; ?>

Numerical experiments: tunable finite-elements

Vary the TimeImplicit parameter $\theta\in[\frac{1}{2};1]$ and the TuneIntegr parameter $p\in]0;1]$ to determine which combination has the smallest numerical damping.

Repeat the study and try to minimize the phase errors.

Introduce a finite physical Diffusion=1 and adjust the TimeImplicit and the TuneIntegr parameters to calculate a solution that is physically meaningful even with a large CFL number.

Having spent a considerable effort understanding the FEM formulation, isn't it frustrating to see how similar the code is to the implicit Crank-Nicholson FD scheme in sect.2.5? This should be the main argument for the community who still uses implicit finite difference schemes: with a little bit of thinking but the same computational cost, the finite element scheme is now considerably more flexibile: it is for example easy to densify the mesh¹⁶, modify the partly implicit time integration from centered to fully implicit $\theta\in[\frac{1}{2};1]$ and tune the integration $p\in[0;1]$ . Convince yourself that Crank-Nicholson (2.5.1#eq.12) and this FEM scheme (3.4#eq.1) are indeed equivalent when using a homogeneous mesh $x_j=j\Delta x$ , a time centered integration $\theta=\frac{1}{2}$ and a trapezoidal quadrature .

SYLLABUS Previous: 3.3 Numerical quadrature Up: 3 FINITE ELEMENT METHOD Next: 3.5 Linear solvers