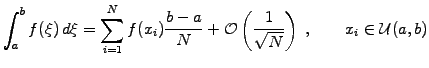','..','$myPermit') ?>
SYLLABUS Previous: 5 MONTE-CARLO METHOD
Up: 5 MONTE-CARLO METHOD
Next: 5.2 Stochastic theory
','..','$myPermit') ?>
SYLLABUS Previous: 5 MONTE-CARLO METHOD
Up: 5 MONTE-CARLO METHOD
Next: 5.2 Stochastic theory
5.1 Monte Carlo integration
Slide : [
integration ||
VIDEO
99) echo "
modem -
ISDN -
LAN
"; else echo "login";?>
]
The most common use of Monte Carlo methods is the evaluation of multi-dimensional integrals [24]. Consider first the approximation of an
integral obtained from the trapezoidal rule (3.3#eq.1)
Instead of a uniform sampling, imagine an evaluation where the positions
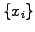 are random numbers uniformly distributed in the
interval
are random numbers uniformly distributed in the
interval ![$ [a,b]$](s5img10.gif) ; this yields a Monte Carlo integration
; this yields a Monte Carlo integration
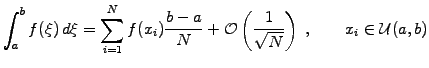 |
(2) |
The convergence rate is of course lower than from a uniform sampling
(5.1#eq.1); the strength however appears for
integrals in higher dimensions 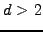 , where the Monte Carlo error scales
as
, where the Monte Carlo error scales
as 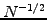 irrespective of the number of dimensions - instead of the
scaling in
irrespective of the number of dimensions - instead of the
scaling in 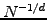 that is achieved when using a uniform mesh.
that is achieved when using a uniform mesh.
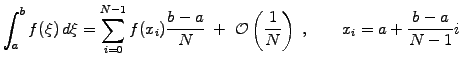


 ','..','$myPermit') ?>
SYLLABUS Previous: 5 MONTE-CARLO METHOD
Up: 5 MONTE-CARLO METHOD
Next: 5.2 Stochastic theory
','..','$myPermit') ?>
SYLLABUS Previous: 5 MONTE-CARLO METHOD
Up: 5 MONTE-CARLO METHOD
Next: 5.2 Stochastic theory