

 Previous: Ad-hoc continuum damping
Up: Shear-Alfvén wavefield & ad-hoc
Next: Ad-hoc complex resistivity
Previous: Ad-hoc continuum damping
Up: Shear-Alfvén wavefield & ad-hoc
Next: Ad-hoc complex resistivity
If a TAE mode is strongly localized within a toroidicity gap and the
peaking of the wavefield such that mode conversion becomes possible
where
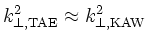 ,
the
amount of power ``radiated away by the kinetic-Alfvén wave'' can be
calculated perturbatively directly from the shear-Alfvén wavefield
[32,33].
Assuming that all the power is finally absorbed in the vicinity of
the conversion region (excluding reflections and fast particle drive
on the kinetic Alfvén wave), the so-called radiative damping has
been evaluated with the NOVA-K code.
Choosing a KAE in JET where the gyrokinetic PENN code
a priori predicted that this particular conversion / damping mechanism
is dominant (Fig.1 in Ref.[31]), the radiative damping and the
electron Landau damping obtained from a self-consistent gyrokinetic
description of the global wavefield [35,31] are found to agree
within approximatively 20% [31,35].
The problem with an ad-hoc evaluation of radiative damping is that it
is not a priori possible to know if other conversion mechanism exist
and dominate; choosing another KAE where the PENN code predicts
that conversion takes place because of weak magnetic shear in the core,
order of magnitude discrepancies appear between the damping from the
two codes [35,31].
An ad-hoc radiative damping model is for example unable to reproduce
the isotope scaling from Ref.[11], for which good agreement
has been achieved between PENN and the measurements from JET.
,
the
amount of power ``radiated away by the kinetic-Alfvén wave'' can be
calculated perturbatively directly from the shear-Alfvén wavefield
[32,33].
Assuming that all the power is finally absorbed in the vicinity of
the conversion region (excluding reflections and fast particle drive
on the kinetic Alfvén wave), the so-called radiative damping has
been evaluated with the NOVA-K code.
Choosing a KAE in JET where the gyrokinetic PENN code
a priori predicted that this particular conversion / damping mechanism
is dominant (Fig.1 in Ref.[31]), the radiative damping and the
electron Landau damping obtained from a self-consistent gyrokinetic
description of the global wavefield [35,31] are found to agree
within approximatively 20% [31,35].
The problem with an ad-hoc evaluation of radiative damping is that it
is not a priori possible to know if other conversion mechanism exist
and dominate; choosing another KAE where the PENN code predicts
that conversion takes place because of weak magnetic shear in the core,
order of magnitude discrepancies appear between the damping from the
two codes [35,31].
An ad-hoc radiative damping model is for example unable to reproduce
the isotope scaling from Ref.[11], for which good agreement
has been achieved between PENN and the measurements from JET.


 Previous: Ad-hoc continuum damping
Up: Shear-Alfvén wavefield & ad-hoc
Next: Ad-hoc complex resistivity
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm
Previous: Ad-hoc continuum damping
Up: Shear-Alfvén wavefield & ad-hoc
Next: Ad-hoc complex resistivity
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm


 Previous: Ad-hoc continuum damping
Up: Shear-Alfvén wavefield & ad-hoc
Next: Ad-hoc complex resistivity
Previous: Ad-hoc continuum damping
Up: Shear-Alfvén wavefield & ad-hoc
Next: Ad-hoc complex resistivity


 Previous: Ad-hoc continuum damping
Up: Shear-Alfvén wavefield & ad-hoc
Next: Ad-hoc complex resistivity
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm
Previous: Ad-hoc continuum damping
Up: Shear-Alfvén wavefield & ad-hoc
Next: Ad-hoc complex resistivity
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm