

 Previous: Ad-hoc radiative damping
Up: Shear-Alfvén wavefield & ad-hoc
Next: Electromagnetic gyrokinetics (GK)
Previous: Ad-hoc radiative damping
Up: Shear-Alfvén wavefield & ad-hoc
Next: Electromagnetic gyrokinetics (GK)
It was apparent in (eq.6) how it is possible to form a
4th order equation with a small change to the resistive MHD by adding
an imaginary part to the plasma resistivity [36]:
![\begin{displaymath}
j_\Vert = -\frac{i\omega}{4\pi}\rho_s^2\left(\frac{2\omega}...
..._e}{T_i}\right)}_%
{\mathrm{KAW mock-up}}
\right]
E_\Vert .
\end{displaymath}](img44.gif) |
(6) |
The kinetic-Alfvén wave dispersion and the mode conversion is mocked-up,
keeping a tiny collisional dissipation 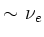 to reproduce weakly
damped KTAE modes that were predicted analytically by Mett & Mahajan
[16].
Implemented in the CASTOR-K code for global wavefields, the
results from the complex resistivity model are however often in
contradiction with the gyrokinetic calculations from the PENN
code. This not surprising, since the dispersion is here not consistent
with the FLR correction
to reproduce weakly
damped KTAE modes that were predicted analytically by Mett & Mahajan
[16].
Implemented in the CASTOR-K code for global wavefields, the
results from the complex resistivity model are however often in
contradiction with the gyrokinetic calculations from the PENN
code. This not surprising, since the dispersion is here not consistent
with the FLR correction
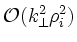 characteristic
of the kinetic-Alfvén wave. The 4th order complex resistivity equation
is very different from a consistent gyrokinetic ordering, the amount of
power converted where the spatial scales match
characteristic
of the kinetic-Alfvén wave. The 4th order complex resistivity equation
is very different from a consistent gyrokinetic ordering, the amount of
power converted where the spatial scales match
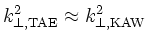 is altered and the Landau damping, which should be a selective 2nd order
differential operator to reproduce the
is altered and the Landau damping, which should be a selective 2nd order
differential operator to reproduce the
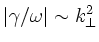 dependence of (eq.2), is entirely absent. This explains
the large qualitative differences between the complex resistivity spectrum
calculated by the CASTOR-K code and the gyrokinetic spectrum.
To our knowledge, it was never possible to show a quantitative agreement
between damping rates predicted using the complex resistivity model and
the measurements from the JET tokamak.
dependence of (eq.2), is entirely absent. This explains
the large qualitative differences between the complex resistivity spectrum
calculated by the CASTOR-K code and the gyrokinetic spectrum.
To our knowledge, it was never possible to show a quantitative agreement
between damping rates predicted using the complex resistivity model and
the measurements from the JET tokamak.


 Previous: Ad-hoc radiative damping
Up: Shear-Alfvén wavefield & ad-hoc
Next: Electromagnetic gyrokinetics (GK)
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm
Previous: Ad-hoc radiative damping
Up: Shear-Alfvén wavefield & ad-hoc
Next: Electromagnetic gyrokinetics (GK)
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm
![\begin{displaymath}
j_\Vert = -\frac{i\omega}{4\pi}\rho_s^2\left(\frac{2\omega}...
..._e}{T_i}\right)}_%
{\mathrm{KAW mock-up}}
\right]
E_\Vert .
\end{displaymath}](img44.gif)


 Previous: Ad-hoc radiative damping
Up: Shear-Alfvén wavefield & ad-hoc
Next: Electromagnetic gyrokinetics (GK)
Previous: Ad-hoc radiative damping
Up: Shear-Alfvén wavefield & ad-hoc
Next: Electromagnetic gyrokinetics (GK)


 Previous: Ad-hoc radiative damping
Up: Shear-Alfvén wavefield & ad-hoc
Next: Electromagnetic gyrokinetics (GK)
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm
Previous: Ad-hoc radiative damping
Up: Shear-Alfvén wavefield & ad-hoc
Next: Electromagnetic gyrokinetics (GK)
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm