

 Previous: Shear-Alfvén wavefield & ad-hoc
Up: Shear-Alfvén wavefield & ad-hoc
Next: Ad-hoc radiative damping
Previous: Shear-Alfvén wavefield & ad-hoc
Up: Shear-Alfvén wavefield & ad-hoc
Next: Ad-hoc radiative damping
The resonance absorption trick [19] has been used to
regularize the MHD singularity when a global wavefield is formed in the
presence of Alfvén resonances; the so-called continuum damping of
AEs has first been computed numerically [26,27],
implemented in the LION and CASTOR codes and solved
analytically [28,29] for radially localized modes.
Using two cold resistive fluids for validation purposes, we repeated
such calculations with the PENN code in Ref.[8] by
writing the current perturbation along the magnetic field as
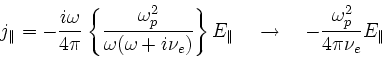 |
(5) |
where the term
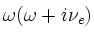 in the denominator is first
replaced by
in the denominator is first
replaced by
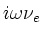 to reduce the 4th order equation in
to reduce the 4th order equation in 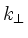 down to 2nd order (neglecting the electron inertia in the momentum
balance) before taking the collisionless limit
down to 2nd order (neglecting the electron inertia in the momentum
balance) before taking the collisionless limit
 .
The large continuum damping
.
The large continuum damping
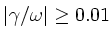 obtained suggested
first that only gap modes (having no intersection with the shear-Alfvén
continuum) can be observed in actual plasmas.
Serious contradictions have been found since both within theory [21]
and the experiments [30,31]; weakly damped modes have been
measured with large fields in the neighborhood of Alfvén resonances with
continuum damping rates exceeding the damping from mode conversion and the
measurements by more than an order of magnitude [30].
Such arguments show that the continuum damping of global AEs is misleading
and that shear-Alfvén continuum plots such as Fig.1 are of
little value to predict the damping and even the existence of AEs.
obtained suggested
first that only gap modes (having no intersection with the shear-Alfvén
continuum) can be observed in actual plasmas.
Serious contradictions have been found since both within theory [21]
and the experiments [30,31]; weakly damped modes have been
measured with large fields in the neighborhood of Alfvén resonances with
continuum damping rates exceeding the damping from mode conversion and the
measurements by more than an order of magnitude [30].
Such arguments show that the continuum damping of global AEs is misleading
and that shear-Alfvén continuum plots such as Fig.1 are of
little value to predict the damping and even the existence of AEs.


 Previous: Shear-Alfvén wavefield & ad-hoc
Up: Shear-Alfvén wavefield & ad-hoc
Next: Ad-hoc radiative damping
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm
Previous: Shear-Alfvén wavefield & ad-hoc
Up: Shear-Alfvén wavefield & ad-hoc
Next: Ad-hoc radiative damping
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm
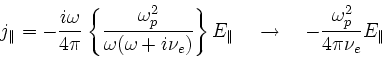


 Previous: Shear-Alfvén wavefield & ad-hoc
Up: Shear-Alfvén wavefield & ad-hoc
Next: Ad-hoc radiative damping
Previous: Shear-Alfvén wavefield & ad-hoc
Up: Shear-Alfvén wavefield & ad-hoc
Next: Ad-hoc radiative damping


 Previous: Shear-Alfvén wavefield & ad-hoc
Up: Shear-Alfvén wavefield & ad-hoc
Next: Ad-hoc radiative damping
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm
Previous: Shear-Alfvén wavefield & ad-hoc
Up: Shear-Alfvén wavefield & ad-hoc
Next: Ad-hoc radiative damping
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm