

 Previous: UNDERLYING PHYSICS
Up: UNDERLYING PHYSICS
Next: Global effects
Previous: UNDERLYING PHYSICS
Up: UNDERLYING PHYSICS
Next: Global effects
MHD, drift, kinetic-Alfvén and resonant wavefields
High frequency 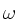 magneto-hydrodynamic (MHD) perturbations
are susceptible to undergo resonant interactions with fast (f)
super-Alfvénic particles
magneto-hydrodynamic (MHD) perturbations
are susceptible to undergo resonant interactions with fast (f)
super-Alfvénic particles
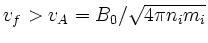 for
frequencies that range roughly from the electron (e) or ion (i)
drift to the Alfvén frequency:
for
frequencies that range roughly from the electron (e) or ion (i)
drift to the Alfvén frequency:
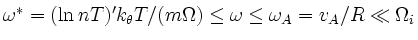 ,
where
,
where
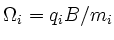 stands
for the cyclotron frequency of the ions.
From a local dispersion analysis of electromagnetic waves, keeping
the pressure gradients and the finite Larmor radius (FLR) of the
ions, it is known that the drift-waves, the kinetic-Alfvén wave
(KAW) and the global MHD wavefield get coupled and yield a relation
of the form
stands
for the cyclotron frequency of the ions.
From a local dispersion analysis of electromagnetic waves, keeping
the pressure gradients and the finite Larmor radius (FLR) of the
ions, it is known that the drift-waves, the kinetic-Alfvén wave
(KAW) and the global MHD wavefield get coupled and yield a relation
of the form
![\begin{displaymath}
\omega^2 -\omega\omega_i^* -v_A^2 k_\Vert^2
\left\{1 + k_\...
...\omega_i^*}{\omega-\omega_e^*}
\right)
\right]
\right\} = 0
\end{displaymath}](img7.gif) |
(1) |
Taking the homogeneous limit
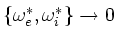 to recover the standard kinetic-Alfvén wave [10], one
immediately sees with Faraday's law how the electrostatic component of
a magnetic perturbation
to recover the standard kinetic-Alfvén wave [10], one
immediately sees with Faraday's law how the electrostatic component of
a magnetic perturbation
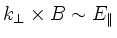 is related to the
ion Larmor radius dispersion term
is related to the
ion Larmor radius dispersion term
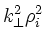 and yields resonant
Landau interactions with passing electrons that move along the magnetic
field lines
and yields resonant
Landau interactions with passing electrons that move along the magnetic
field lines
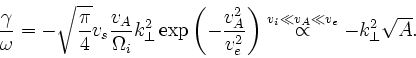 |
(2) |
In the regime typical of tokamaks nowadays, the Alfvén velocity lies
between the ion vi and electron thermal velocities ve, so that
for a fixed mode structure 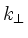 and similar plasma conditions,
the electron Landau damping is proportional to the square root of the
isotope mass
and similar plasma conditions,
the electron Landau damping is proportional to the square root of the
isotope mass 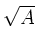 ;
this argument has recently been tested against
the experiment [11]. Damping occurs also via the collisions
between passing or trapped electrons [12,13], but
this collisional damping is negligible compared with the electron Landau
damping for fusion relevant regimes - as will be substantiated below in
answer to [1].
;
this argument has recently been tested against
the experiment [11]. Damping occurs also via the collisions
between passing or trapped electrons [12,13], but
this collisional damping is negligible compared with the electron Landau
damping for fusion relevant regimes - as will be substantiated below in
answer to [1].
If the inhomogeneity drifts become sufficiently large
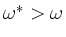 ,
the kinetic energy of the particles may be transferred to the wave and
provides a finite drive that may overcome the total damping.
This can under circumstance occur for the bulk species, but is most
easily achieved by fast (energetic) ions. Substituting
,
the kinetic energy of the particles may be transferred to the wave and
provides a finite drive that may overcome the total damping.
This can under circumstance occur for the bulk species, but is most
easily achieved by fast (energetic) ions. Substituting
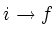 in (eq.1) when the fast particle pressure gradient dominates
the ions response
in (eq.1) when the fast particle pressure gradient dominates
the ions response
 ,
it is clear that the
wavefield acquires a resonant or energetic character when the normalized
fast particle pressure
,
it is clear that the
wavefield acquires a resonant or energetic character when the normalized
fast particle pressure
 is comparable
with the bulk
is comparable
with the bulk 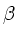 .
.


 Previous: UNDERLYING PHYSICS
Up: UNDERLYING PHYSICS
Next: Global effects
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm
Previous: UNDERLYING PHYSICS
Up: UNDERLYING PHYSICS
Next: Global effects
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm
![\begin{displaymath}
\omega^2 -\omega\omega_i^* -v_A^2 k_\Vert^2
\left\{1 + k_\...
...\omega_i^*}{\omega-\omega_e^*}
\right)
\right]
\right\} = 0
\end{displaymath}](img7.gif)


 Previous: UNDERLYING PHYSICS
Up: UNDERLYING PHYSICS
Next: Global effects
Previous: UNDERLYING PHYSICS
Up: UNDERLYING PHYSICS
Next: Global effects
![]() ,
the kinetic energy of the particles may be transferred to the wave and
provides a finite drive that may overcome the total damping.
This can under circumstance occur for the bulk species, but is most
easily achieved by fast (energetic) ions. Substituting
,
the kinetic energy of the particles may be transferred to the wave and
provides a finite drive that may overcome the total damping.
This can under circumstance occur for the bulk species, but is most
easily achieved by fast (energetic) ions. Substituting
![]() in (eq.1) when the fast particle pressure gradient dominates
the ions response
in (eq.1) when the fast particle pressure gradient dominates
the ions response
![]() ,
it is clear that the
wavefield acquires a resonant or energetic character when the normalized
fast particle pressure
,
it is clear that the
wavefield acquires a resonant or energetic character when the normalized
fast particle pressure
![]() is comparable
with the bulk
is comparable
with the bulk ![]() .
.


 Previous: UNDERLYING PHYSICS
Up: UNDERLYING PHYSICS
Next: Global effects
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm
Previous: UNDERLYING PHYSICS
Up: UNDERLYING PHYSICS
Next: Global effects
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm