

 Previous: MHD, drift, kinetic-Alfvén and
Up: UNDERLYING PHYSICS
Next: Mode conversion
Previous: MHD, drift, kinetic-Alfvén and
Up: UNDERLYING PHYSICS
Next: Mode conversion
If the equilibrium scale length become sizable when measured in terms of the
perturbation wavelength, global effects lead to important modifications
of the local dispersion properties. Take for example the shear-Alfvén
wave ({
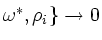 in eq.1) in a
tokamak, use a Fourier decomposition toroidally
in eq.1) in a
tokamak, use a Fourier decomposition toroidally
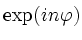 and
poloidally
and
poloidally
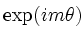 in order to obtain an algebraic representation
of the parallel wave vector
in order to obtain an algebraic representation
of the parallel wave vector
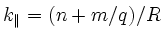 .
Fig.1 illustrates how different harmonics get coupled and
yield so-called BAE, TAE, EAE gaps where the plasma beta, the toroidicity
and ellipticity prevent shear-Alfvén waves of any frequency from
propagating over large portions of the minor radius.
Global (radially extended,
.
Fig.1 illustrates how different harmonics get coupled and
yield so-called BAE, TAE, EAE gaps where the plasma beta, the toroidicity
and ellipticity prevent shear-Alfvén waves of any frequency from
propagating over large portions of the minor radius.
Global (radially extended,
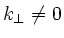 )
solutions however exist within
these gaps, the so-called Alfvén eigenmodes (AEs): they often have a
mixed T/EAE character and require a global calculation to determine the
mode structure
)
solutions however exist within
these gaps, the so-called Alfvén eigenmodes (AEs): they often have a
mixed T/EAE character and require a global calculation to determine the
mode structure
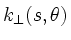 and the corresponding damping / drive.
and the corresponding damping / drive.
Figure 1:
Global effects on the shear-Alfvén wave dispersion.
|
|
Global effects modify also the kinetic-Alfvén and the drift waves, which
finally get combined with AE wavefields into what we call kinetic AEs
(KAEs) [14] and drift-kinetic AEs (DKAEs) [15].
In this sense, Mett & Mahajan's KTAEs [16] are a special type of
KAEs that involve only the kinetic-Alfvén wave.
Finally, when the energetic particle character dominates the ion response,
global solutions exist also for the resonant wavefield and are generally
referred to as energetic particle modes (EPMs) [17].


 Previous: MHD, drift, kinetic-Alfvén and
Up: UNDERLYING PHYSICS
Next: Mode conversion
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm
Previous: MHD, drift, kinetic-Alfvén and
Up: UNDERLYING PHYSICS
Next: Mode conversion
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm
![\includegraphics[height=8cm]{FIG/gapITERn12.ps}](img25.gif)


 Previous: MHD, drift, kinetic-Alfvén and
Up: UNDERLYING PHYSICS
Next: Mode conversion
Previous: MHD, drift, kinetic-Alfvén and
Up: UNDERLYING PHYSICS
Next: Mode conversion


 Previous: MHD, drift, kinetic-Alfvén and
Up: UNDERLYING PHYSICS
Next: Mode conversion
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm
Previous: MHD, drift, kinetic-Alfvén and
Up: UNDERLYING PHYSICS
Next: Mode conversion
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm