

 Previous: Mode conversion
Up: UNDERLYING PHYSICS
Next: GLOBAL MODES & DAMPING
Previous: Mode conversion
Up: UNDERLYING PHYSICS
Next: GLOBAL MODES & DAMPING
Following the local analysis from sect.2.1, a harmonic
oscillation
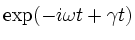 is locally unstable if the
drive exceeds the damping
is locally unstable if the
drive exceeds the damping
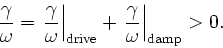 |
(3) |
This criterion is extended to global modes by measuring the total power
transfer from the particles to the wavefield
Ptot=Pf+Pe+Pi:
normalizing with respect to the wave reactive power 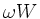 ,
a global
instability occurs if
,
a global
instability occurs if
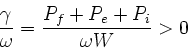 |
(4) |
i.e. when a net power flows from the particles to the wavefield and
amplifies an initial perturbation.
This criterion remains valid in the presence of mode conversion as seen
for example with the DKAE instabilities in DIII-D [15],
where power flows from the AE wavefield to an electromagnetic drift wave
that is Landau damped locally by the electrons, and simultaneously channels
from the fast ions driving this drift wave back to the global wavefield
to be driven in fact through the conversion layer.
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm


 Previous: Mode conversion
Up: UNDERLYING PHYSICS
Next: GLOBAL MODES & DAMPING
Previous: Mode conversion
Up: UNDERLYING PHYSICS
Next: GLOBAL MODES & DAMPING