

 ','..','$myPermit') ?>
SYLLABUS Previous: 1.3.1 Advection
Up: 1.3 Prototype problems
Next: 1.3.3 Dispersion
','..','$myPermit') ?>
SYLLABUS Previous: 1.3.1 Advection
Up: 1.3 Prototype problems
Next: 1.3.3 Dispersion
1.3.2 Diffusion
Slide : [
diffusion -
Green function ||
VIDEO
99) echo "
modem -
ISDN -
LAN
"; else echo "login";?>
]
At the microscopic scale, diffusion is in fact related to a
random motion leading to the prototype equation (exercise 1.04)
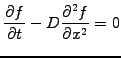 |
(1.3.2#eq.1) |
where 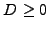 is the diffusion coefficient.
For a homogeneous medium, the combined advection-diffusion equation
is the diffusion coefficient.
For a homogeneous medium, the combined advection-diffusion equation
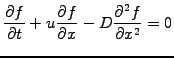 |
(1.3.2#eq.2) |
can be solved analytically in terms of the Green function
(exercise 1.03)
A numerical solution is generally required to solve the equation in an
inhomogeneous medium, where 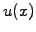 ,
, 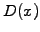
Below is an example of a
numerical solution describing the diffusion of an initial box function
computed using the finite element method from chapter 3.
JBONE applet: press Start/Stop
to simulate the diffusion of a box function in a periodic domain.
|
|
"; ?>
A harmonic ansatz
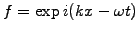 can be used to analyze the
diffusion equation and leads to the dispersion relation
can be used to analyze the
diffusion equation and leads to the dispersion relation
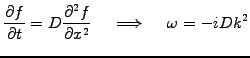 |
(1.3.2#eq.4) |
This shows that short wavelengths (large 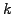 ) are more strongly damped
(large negative imaginary
) are more strongly damped
(large negative imaginary 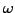 ) than long wavelengths, with a decay
rate proportional to
) than long wavelengths, with a decay
rate proportional to
![$ exp[-i\omega t]=\exp [-D k^2 t]$](s1img95.gif) .
This explains the numerical experiments above.
.
This explains the numerical experiments above.
Note that the heat equation, which describes the evolution of the
temperature 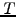 in a medium with a heat conductivity
in a medium with a heat conductivity 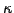 in the
presence of heat sources and sinks
in the
presence of heat sources and sinks 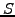
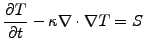 |
(1.3.2#eq.5) |
is one particular application of the diffusion equation. It can easily be
reduced to (1.3.2#eq.1) by substituting the differential operator
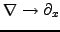 in cartesian coordinates for a 1D slab.
in cartesian coordinates for a 1D slab.
SYLLABUS Previous: 1.3.1 Advection
Up: 1.3 Prototype problems
Next: 1.3.3 Dispersion
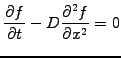


 ','..','$myPermit') ?>
SYLLABUS Previous: 1.3.1 Advection
Up: 1.3 Prototype problems
Next: 1.3.3 Dispersion
','..','$myPermit') ?>
SYLLABUS Previous: 1.3.1 Advection
Up: 1.3 Prototype problems
Next: 1.3.3 Dispersion
![]() can be used to analyze the
diffusion equation and leads to the dispersion relation
can be used to analyze the
diffusion equation and leads to the dispersion relation
![]() in a medium with a heat conductivity
in a medium with a heat conductivity ![]() in the
presence of heat sources and sinks
in the
presence of heat sources and sinks ![]()