

 ','..','$myPermit') ?>
SYLLABUS Previous: 1.3.2 Diffusion
Up: 1.3 Prototype problems
Next: 1.3.4 Wave-breaking
','..','$myPermit') ?>
SYLLABUS Previous: 1.3.2 Diffusion
Up: 1.3 Prototype problems
Next: 1.3.4 Wave-breaking
1.3.3 Dispersion
Slide : [
dispersion ||
VIDEO
99) echo "
modem -
ISDN -
LAN
"; else echo "login";?>
]
Dispersion occurs when different wavelengths propagate with different
phase velocities. Take for example a third order dispersion equation
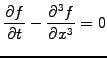 |
(1.3.3#eq.1) |
The harmonic ansatz in space and time
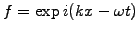 shows that
the phase velocity
shows that
the phase velocity
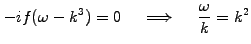 |
(1.3.3#eq.2) |
is larger for short wavelengths (large 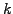 propagate faster) than long
wavelengths (small
propagate faster) than long
wavelengths (small 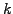 propagate slower).
In the Korteweg-DeVries equation, this will explain why
large amplitude solitons with short wavelengths propagate more
rapidly than low amplitudes solitons having long wavelengths.
propagate slower).
In the Korteweg-DeVries equation, this will explain why
large amplitude solitons with short wavelengths propagate more
rapidly than low amplitudes solitons having long wavelengths.
Unfortunately, dispersion does not always have a physical origin: remember
(1.2.4#eq.3), showing how a centered finite difference approximation
under-estimates first order derivatives of short wavelengths.
This is exactly what happens in the 3 levels scheme for
the advection equation, where different Fourier components included in the
initial square box function propagate with different velocities.
JBONE applet: press Start/Stop
to observe how the numerical dispersion induced from a finite
difference approximation affects the advection of a square pulse.
|
|
"; ?>
Numerical dispersion affects almost every approximation that will be
discussed in this course. It is therefore important to ensure that
numerical solutions reproduce the physical dispersion and not the
spurious numerical dispersion introduced by the discretisation.
SYLLABUS Previous: 1.3.2 Diffusion
Up: 1.3 Prototype problems
Next: 1.3.4 Wave-breaking
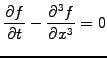


 ','..','$myPermit') ?>
SYLLABUS Previous: 1.3.2 Diffusion
Up: 1.3 Prototype problems
Next: 1.3.4 Wave-breaking
','..','$myPermit') ?>
SYLLABUS Previous: 1.3.2 Diffusion
Up: 1.3 Prototype problems
Next: 1.3.4 Wave-breaking