

 ','..','$myPermit') ?>
SYLLABUS Previous: 2.1 Explicit 2 levels
Up: 2 FINITE DIFFERENCES
Next: 2.3 Lax-Wendroff
','..','$myPermit') ?>
SYLLABUS Previous: 2.1 Explicit 2 levels
Up: 2 FINITE DIFFERENCES
Next: 2.3 Lax-Wendroff
2.2 Explicit 3 levels
Slide : [ 3 levels
Scheme -
Code -
Run ||
VIDEO
99) echo "
modem -
ISDN -
LAN
"; else echo "login";?>
]
A more accurate scheme in
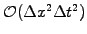 is obtained
from centered differences
is obtained
from centered differences
Figure 2.2#fig.3:
Explicit 3 levels.
|
|
![$\displaystyle f_j^{t+\Delta t} = f_j^{t-\Delta t} - \beta\left[ f_{j+1}^t - f_{j-1}^t \right] + 2\alpha\left[ f_{j+1}^t -2f_j^t +f_{j-1}^t\right]$](s2img53.gif) |
(2.2.0#eq.5) |
The scheme involves three time levels (fm[j], f[j], fp[j]) and has been
implemented in JBONE
as
for (int j=1; j<n; j++) {
fp[j]=fm[j] -beta*(f[j+1]-f[j-1]) +2*alpha*(f[j+1]-2.*f[j]+f[j-1]);}
fp[0]=fm[0] -beta*(f[ 1 ]-f[ n ]) +2*alpha*(f[ 1 ]-2.*f[0]+f[ n ]);
fp[n]=fm[n] -beta*(f[ 0 ]-f[n-1]) +2*alpha*(f[ 0 ]-2.*f[n]+f[n-1]);
A special
starting procedure
is required to calculate an approximation at a time 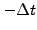 anterior
to the initial condition
anterior
to the initial condition  . This can be implemented by taking one
step backwards in time with the explicit 2 levels scheme (2.1#eq.1).
The example below
shows the result obtained using the same parameters for the advection
equation as in the previous section.
. This can be implemented by taking one
step backwards in time with the explicit 2 levels scheme (2.1#eq.1).
The example below
shows the result obtained using the same parameters for the advection
equation as in the previous section.
JBONE applet: press Start/Stop
to simulate the advection of a box function and to test how the
explicit 3 levels scheme affects the dispersion and the damping
of short and long wavelengths superposed in a box function.
|
|
"; ?>
Despite the mathematically higher accuracy in
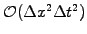 and the excellent conservation of the
lowest order moment,
the initial box function is strongly distorted by the phase errors
created from numerical dispersion, when short wavelengths propagate
at a different speed from longuer wavelengths due to inaccuracies in the
finite difference approximations.
and the excellent conservation of the
lowest order moment,
the initial box function is strongly distorted by the phase errors
created from numerical dispersion, when short wavelengths propagate
at a different speed from longuer wavelengths due to inaccuracies in the
finite difference approximations.
Because the numerical dispersion slows down short wavelengths
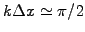 , the solution can become locally negative
even if it was strictly positive at the beginning.
This is of course not physical and can be a problem if
, the solution can become locally negative
even if it was strictly positive at the beginning.
This is of course not physical and can be a problem if 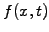 is a
density... Low numerical damping, however, makes the 3 levels scheme
attractive when a simple solution is sought only for advection.
The choice between a 2 or 3 level scheme ultimately depends on the
specific application and always implies a sound monitoring of the
numerical parameters at run time.
is a
density... Low numerical damping, however, makes the 3 levels scheme
attractive when a simple solution is sought only for advection.
The choice between a 2 or 3 level scheme ultimately depends on the
specific application and always implies a sound monitoring of the
numerical parameters at run time.
SYLLABUS Previous: 2.1 Explicit 2 levels
Up: 2 FINITE DIFFERENCES
Next: 2.3 Lax-Wendroff


 ','..','$myPermit') ?>
SYLLABUS Previous: 2.1 Explicit 2 levels
Up: 2 FINITE DIFFERENCES
Next: 2.3 Lax-Wendroff
','..','$myPermit') ?>
SYLLABUS Previous: 2.1 Explicit 2 levels
Up: 2 FINITE DIFFERENCES
Next: 2.3 Lax-Wendroff
![]() is obtained
from centered differences
is obtained
from centered differences
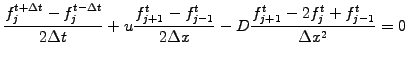
![]() , the solution can become locally negative
even if it was strictly positive at the beginning.
This is of course not physical and can be a problem if
, the solution can become locally negative
even if it was strictly positive at the beginning.
This is of course not physical and can be a problem if ![]() is a
density... Low numerical damping, however, makes the 3 levels scheme
attractive when a simple solution is sought only for advection.
The choice between a 2 or 3 level scheme ultimately depends on the
specific application and always implies a sound monitoring of the
numerical parameters at run time.
is a
density... Low numerical damping, however, makes the 3 levels scheme
attractive when a simple solution is sought only for advection.
The choice between a 2 or 3 level scheme ultimately depends on the
specific application and always implies a sound monitoring of the
numerical parameters at run time.