1.4.5 Harmonic functions

SYLLABUS Previous: 1.4.4 Splines Up: 1.4 Numerical discretization Next: 1.4.6 Wavelets

1.4.5 Harmonic functions

A harmonic decomposition is obtained from a discrete Fourier transform (DFT) assuming a regular mesh and a periodic domain of length . Using the notations $x_m=m\Delta x=m L/M$ and $k_m=2\pi m /L$ , the forward and backward transformations are defined as

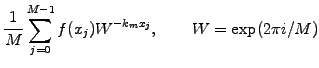$\displaystyle \widehat{f}(k_m)$	$\displaystyle =$	$\displaystyle \frac{1}{M}\sum_{j=0}^{M-1} f(x_j) W^{-k_m x_j},\quad\quad W=\exp(2\pi i/M)$	(1.4.5#eq.1)
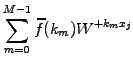$\displaystyle f(x_j)$	$\displaystyle =$	$\displaystyle \sum_{m=0}^{M-1} \widehat{f}(k_m) W^{+k_m x_j}$	(1.4.5#eq.2)

is a power of 2, the total number of operations can be dramatically reduced from

to $M\log_2 M$ in a fast Fourier transform (FFT), by applying recursively the decomposition

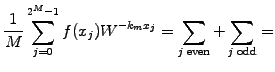$\displaystyle \widehat{f}(k_m)$	$\displaystyle =$	$\displaystyle \frac{1}{M}\sum_{j=0}^{2^M-1} f(x_j) W^{-k_m x_j} = \sum_{j\;\mathrm{even}} +\sum_{j\;\mathrm{odd}} =$
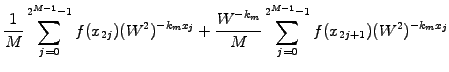	$\displaystyle =$	$\displaystyle \frac{1}{M}\sum_{j=0}^{2^{M-1}-1} f(x_{2j}) (W^2)^{-k_m x_j} +\frac{W^{-k_m}}{M}\sum_{j=0}^{2^{M-1}-1} f(x_{2j+1})(W^2)^{-k_m x_j}$

with $W^2=\exp(2i\pi/2^{M-1})$ until a sum of DFT of length

is obtained. Figure (1.4.5#fig.1) illustrates how the approximation of a periodic square wave converges with an increasing number of Fourier components. Note how the function overshoots in the neighborhood of sharp edges: this is the Gibbs phenomenon and it will always be there for a finite number of terms in the sum.

**Figure:** Square wave $\displaystyle\sum_{m=0}^M \frac{2}{\pi(2m+1)}\sin\left(\frac{(2m+1)\pi x}{L}\right)$ with .
$\includegraphics[width=10cm]{figs/AprxFFT.psc}$

It should not be surprizing to hear that a harmonic decomposition is particularly well suited for smooth global functions with long wavelengths $\lambda\sim L$ , since they result in a narrow spectrum $\vert k\vert\le 2\pi/\lambda\ll \pi/\Delta x$ . Note that the convergence with an increasing number of Fourier components is faster than any polynomial once the smallest structure has been resolved. The implementation of non-periodic boundary conditions, however, can sometimes be problematic.

SYLLABUS Previous: 1.4.4 Splines Up: 1.4 Numerical discretization Next: 1.4.6 Wavelets