

 ','..','$myPermit') ?>
SYLLABUS Previous: 1.3.5 Schrödinger
Up: 1 INTRODUCTION
Next: 1.4.1 Convergence, Richardson extrapolation
','..','$myPermit') ?>
SYLLABUS Previous: 1.3.5 Schrödinger
Up: 1 INTRODUCTION
Next: 1.4.1 Convergence, Richardson extrapolation
1.4 Numerical discretization
Slide : [
mesh -
roof-top -
spline -
harmonic -
wavelets -
particles ||
VIDEO
99) echo "
modem -
ISDN -
LAN
"; else echo "login";?>
]
Numerical solutions are obtained by evolving a discrete set of values
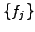 ,
, 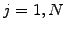 with small steps in time
with small steps in time 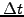 to approximate
what really should be a continuous function of space and time
to approximate
what really should be a continuous function of space and time 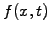 ,
,
![$ x\in[a;b]$](s1img126.gif) ,
, 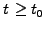 . Unfortunately, there is no universal method.
Rather than blindly adopting a local favorite, your choice really
should depend on
. Unfortunately, there is no universal method.
Rather than blindly adopting a local favorite, your choice really
should depend on
- the structure of the solution (continuity, regularity, precision),
post-processing (filters) and the diagnostics (Fourier spectrum)
that are expensive but might be required anyway,
- the boundary conditions that can be difficult to implement in some
methods,
- the structure of the differential operator (the analytic formulation,
the computational cost in memory
 time, the numerical stability)
and the computer architecture (vectorization, parallelization).
time, the numerical stability)
and the computer architecture (vectorization, parallelization).
This course is a lot about advantages and limitations from a variety
of methods.
By analyzing model problems in a simple 1D slab, you learn the tricks
that are important to know before you work with a higher number of
dimensions.
The broader perspective allows you to choose an optimal solution, where
you can exploit the advantages and work around the limitations for your
particular problem.
Subsections
SYLLABUS Previous: 1.3.5 Schrödinger
Up: 1 INTRODUCTION
Next: 1.4.1 Convergence, Richardson extrapolation


 ','..','$myPermit') ?>
SYLLABUS Previous: 1.3.5 Schrödinger
Up: 1 INTRODUCTION
Next: 1.4.1 Convergence, Richardson extrapolation
','..','$myPermit') ?>
SYLLABUS Previous: 1.3.5 Schrödinger
Up: 1 INTRODUCTION
Next: 1.4.1 Convergence, Richardson extrapolation
![]() ,
, ![]() with small steps in time
with small steps in time ![]() to approximate
what really should be a continuous function of space and time
to approximate
what really should be a continuous function of space and time ![]() ,
,
![]() ,
, ![]() . Unfortunately, there is no universal method.
Rather than blindly adopting a local favorite, your choice really
should depend on
. Unfortunately, there is no universal method.
Rather than blindly adopting a local favorite, your choice really
should depend on