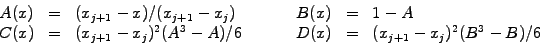','..','$myPermit') ?>
SYLLABUS Previous: 1.4.3 Finite elements
Up: 1.4 Numerical discretization
Next: 1.4.5 Harmonic functions
','..','$myPermit') ?>
SYLLABUS Previous: 1.4.3 Finite elements
Up: 1.4 Numerical discretization
Next: 1.4.5 Harmonic functions
1.4.4 Splines
Starting from an approximation on an inhomogeneous mesh, the idea of
splines is to provide a global interpolation that is continuous up to
a certain derivative.
For example, take a cubic Hermite spline with the 4 parameters
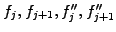 , which
completely determine all 4 coefficients of the cubic polynomial
, which
completely determine all 4 coefficients of the cubic polynomial
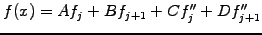 |
(1.4.4#eq.1) |
It is straight forward to calculate the first and second derives
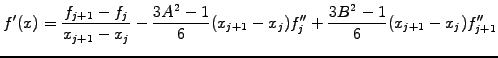 |
(1.4.4#eq.2) |
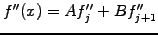 |
(1.4.4#eq.3) |
Starting with only sampled values and no information about the curvature,
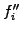 are usually calculated so as to guarantee a smooth
interpolation. Most common is to require that
are usually calculated so as to guarantee a smooth
interpolation. Most common is to require that
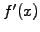 be continuous
from one interval to the next, leading to a tridiagonal system that holds
for
be continuous
from one interval to the next, leading to a tridiagonal system that holds
for 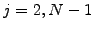
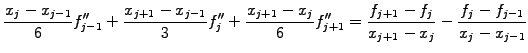 |
(1.4.4#eq.4) |
and can be solved efficiently with
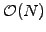 operations.
Two free parameters at the boundaries are used to impose the
boundary conditions by choosing
operations.
Two free parameters at the boundaries are used to impose the
boundary conditions by choosing
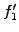 and
and
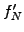 (1.4.4#eq.2).
(1.4.4#eq.2).
Figure:
Approximation of 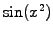 with cubic Hermite splines.
with cubic Hermite splines.
|
|
Figure (1.4.4#fig.1) illustrates the procedure and shows the excellent
quality of a cubic approximation until it breaks down at the limit of 2
mesh points per wavelength.
SYLLABUS Previous: 1.4.3 Finite elements
Up: 1.4 Numerical discretization
Next: 1.4.5 Harmonic functions


 ','..','$myPermit') ?>
SYLLABUS Previous: 1.4.3 Finite elements
Up: 1.4 Numerical discretization
Next: 1.4.5 Harmonic functions
','..','$myPermit') ?>
SYLLABUS Previous: 1.4.3 Finite elements
Up: 1.4 Numerical discretization
Next: 1.4.5 Harmonic functions
![]() , which
completely determine all 4 coefficients of the cubic polynomial
, which
completely determine all 4 coefficients of the cubic polynomial