

 ','..','$myPermit') ?>
SYLLABUS Previous: 1.4.6 Wavelets
Up: 1.4 Numerical discretization
Next: 1.5 Computer quiz
','..','$myPermit') ?>
SYLLABUS Previous: 1.4.6 Wavelets
Up: 1.4 Numerical discretization
Next: 1.5 Computer quiz
1.4.7 Sampling with quasi-particles
A completely different way of approximating a function is to use a
statistical sampling with quasi-particles
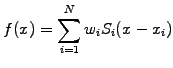 |
(1.4.7#eq.1) |
where 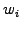 is the weight,
is the weight, 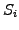 the shape, and
the shape, and 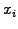 the position of
each particle.
In the JBONE applet, the particle shapes are assumed to be
Dirac pulses
the position of
each particle.
In the JBONE applet, the particle shapes are assumed to be
Dirac pulses
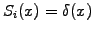 , meaning that the particles are
localized in an infinitely small interval around
, meaning that the particles are
localized in an infinitely small interval around 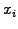
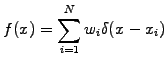 |
(1.4.7#eq.2) |
For simplicity, the weight is often set to unity
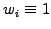 .
As a matter of fact, this form of discretization does never converge
locally, since the Dirac pulses are either zero or infinite.
However, the ``global properties'' (or moments) of a smooth and
bounded function
.
As a matter of fact, this form of discretization does never converge
locally, since the Dirac pulses are either zero or infinite.
However, the ``global properties'' (or moments) of a smooth and
bounded function 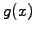 discretized with Dirac pulses does converge
discretized with Dirac pulses does converge
Without a local convergence, it is of course difficult to compare a
quasi-particle discretization with a different approximation, based for
example on finite elements. The particle solution is therefore
projected
onto a set of basis functions
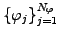 in an
assignment process, which attributes a statistical average to a grid:
in an
assignment process, which attributes a statistical average to a grid:
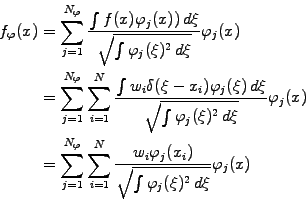 |
(1.4.7#eq.3) |
In JBONE, the projecting basis functions are piecewise linear
roof-top functions.
Note that it is important to use the same set of functions for the
projection and the plot: figure (1.4.7#fig.1) shows how
a Gaussian particle distribution appears after projection, when the
result is plotted using piecewise constant (box) and linear (roof-top)
functions. The dashed line incorrectly mixes boxes for the projection
with roof-tops for the plot.
Figure 1.4.7#fig.1:
The solid lines are legitimate projections of a Gaussian particle
distribution on piecewise constant (box) and linear (roof-top) basis
functions. The dashed line illustrates what happens if boxes are used for
the projection and mistakenly mixed with roof-tops for the plot.
|
|
Try to press INITIALIZE a
few times to get a feeling how good a quasi-particle approximation is to
approximate a box with 64 grid points and a varying number of particles
(random walkers).
You need however to be patient if you exceed 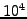 particles... the
JAVA virtual machines in the web browsers are usually rather
slow!
particles... the
JAVA virtual machines in the web browsers are usually rather
slow!
JBONE applet: press Initialize
to approximate the initial Gaussian (grey) with a finite number
of particles or random walkers.
Vary the number of Walkers in the range [1;10000] to get a
feeling for the statistical noise that is associated with such an
approximation; switch to Particle methods to avoid plotting
the particles in red.
|
|
"; ?>
The applet uses random numbers to generate a particle distribution from the
initial condition 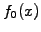 with a
range
with a
range
![$ \left[f_{\text{min}}, f_{\text{max}}\right]$](s1img239.gif) in the interval
in the interval ![$ [a,b]$](s1img240.gif) following the procedure
following the procedure
Let 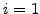
while
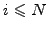
 Let
Let 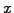 be a uniformly distributed random number in
the interval
be a uniformly distributed random number in
the interval ![$ [a,b]$](s1img240.gif) .
.
 Let
Let 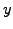 be a uniformly distributed random number in
the interval
be a uniformly distributed random number in
the interval
![$ \left[f_{\text{min}}, f_{\text{max}}\right]$](s1img239.gif) .
.
 If
If
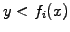 then let
then let 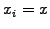 and
advance
and
advance 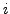 by 1 else do nothing.
by 1 else do nothing.
end while
This algorithm produces a particle density in the interval ![$ [a; b]$](s1img247.gif) that is proportional to the initial condition
that is proportional to the initial condition
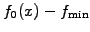 .
.
SYLLABUS Previous: 1.4.6 Wavelets
Up: 1.4 Numerical discretization
Next: 1.5 Computer quiz
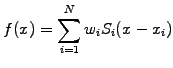


 ','..','$myPermit') ?>
SYLLABUS Previous: 1.4.6 Wavelets
Up: 1.4 Numerical discretization
Next: 1.5 Computer quiz
','..','$myPermit') ?>
SYLLABUS Previous: 1.4.6 Wavelets
Up: 1.4 Numerical discretization
Next: 1.5 Computer quiz
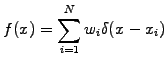
![\includegraphics[width=8cm]{figs/ProjectionBase.eps}](s1img236.gif)
![]() particles... the
JAVA virtual machines in the web browsers are usually rather
slow!
particles... the
JAVA virtual machines in the web browsers are usually rather
slow!
Let
be a uniformly distributed random number in the interval
.
Let
be a uniformly distributed random number in the interval
.
If
then let
and advance
by 1 else do nothing.