

 ','..','$myPermit') ?>
SYLLABUS Previous: 2 FINITE DIFFERENCES
Up: 2 FINITE DIFFERENCES
Next: 2.2 Explicit 3 levels
','..','$myPermit') ?>
SYLLABUS Previous: 2 FINITE DIFFERENCES
Up: 2 FINITE DIFFERENCES
Next: 2.2 Explicit 3 levels
2.1 Explicit 2 levels
Slide : [ 2 levels
Scheme -
Code -
Run -
Stability -
Upwind ||
VIDEO
99) echo "
modem -
ISDN -
LAN
"; else echo "login";?>
]
A spatial difference to the left for the advection (1.3.1#eq.1)
and a centered difference for the diffusion (1.3.2#eq.1) for
example yields an explicit scheme for the advection-diffusion equation
that involves only two time levels
Figure 2.1#fig.1:
Explicit 2 levels.
|
|
The Courant-Friedrichs-Lewy (CFL) number
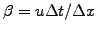 and the coefficient
and the coefficient
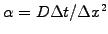 measure typical advection and
diffusion velocities relative to the characteristic propagation
speed of the mesh
measure typical advection and
diffusion velocities relative to the characteristic propagation
speed of the mesh
 .
For every step in time, a new value of the solution
.
For every step in time, a new value of the solution fp[j] is
obtained explicitly from a linear combination involving the nearest
neighbors f[j-1],f[j],f[j+1], which are known either from a
previous step or the initial condition. This scheme has been
implemented in JBONE
as
for (int j=1; j<n; j++) {
fp[j]=f[j] -beta *(f[j]-f[j-1])+alpha*(f[j+1]-2.*f[j]+f[j-1]); }
fp[0]=f[0] -beta *(f[0]-f[ n ])+alpha*(f[ 1 ]-2.*f[0]+f[ n ]);
fp[n]=f[n] -beta *(f[n]-f[n-1])+alpha*(f[ 0 ]-2.*f[n]+f[n-1]);
where the last two statements take care of the periodicity.
Sharp variations of the solution should be AVOIDED to produce
physically meaningful results; to study the numerical properties of
a approximation, it is however often illuminating to initialize a
box function
and check how the intrinsic numerical dispersion / damping of a
scheme affects the superposition of both the short and the long
wavelengths.
The example below
shows the result of an evolution with a constant advection  and
no physical diffusion
and
no physical diffusion
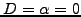 .
.
JBONE applet: press Start/Stop
to simulate the advection of a box function and to test how the
explicit 2 levels scheme affects the dispersion and the damping
of short and long wavelengths superposed in a box function.
|
|
"; ?>
After 128 steps of duration
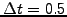 , the pulse propagates exactly
once accross the periodic domain, which is here discretized with 64 mesh
points homogeneously distributed over the length
, the pulse propagates exactly
once accross the periodic domain, which is here discretized with 64 mesh
points homogeneously distributed over the length 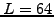 so that
so that
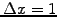 .
The lowest order
moment
(density, (1.2.5#eq.1)) is conserved to a very good accuracy
(as can be judged from the JBONE monitor under
.
The lowest order
moment
(density, (1.2.5#eq.1)) is conserved to a very good accuracy
(as can be judged from the JBONE monitor under Mom[%])
and the function remains positive everywhere as it should(as can be judged from Min)
. The shape, however, is strongly affected as the sharp edges are smoothed
out due intrinsic numerical damping.
The properties of a FD approximation are best understood from a
numerical dispersion / Von Neuman stability analysis, which
is carried out on a homogeneous grid
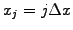 using a
hamonic ansatz
using a
hamonic ansatz
![$ f \sim F=\exp(i[kx-\omega t])$](s2img28.gif) .
Define the amplification factor as
.
Define the amplification factor as
and simplify by 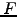 to cast the dispersion relation into
to cast the dispersion relation into
Figure 2.1#fig.2 illustrates with vectors in the complex plane
how the first three term are combined in the presence of advection only
(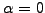 ).
).
Figure 2.1#fig.2:
Numerical dispersion / stability (explicit 2 levels).
|
|
Short wavelengths
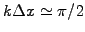 are heavily damped
are heavily damped 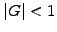 (area inside the outer circle) if the CFL number is smaller than unity
(area inside the outer circle) if the CFL number is smaller than unity
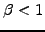 ; for values exceeding the magic time step where
; for values exceeding the magic time step where 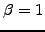 ,
the short wavelengths however grow into a so-called numerical
instability.
Reload
the initial applet
parameters and try to reproduce this in JBONE.
,
the short wavelengths however grow into a so-called numerical
instability.
Reload
the initial applet
parameters and try to reproduce this in JBONE.
For a diffusive process (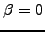 ), the dispersion relation
(2.1#eq.3) shows that the 2 levels scheme is stable for
all wavelengths provided that
), the dispersion relation
(2.1#eq.3) shows that the 2 levels scheme is stable for
all wavelengths provided that
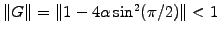 ,
i.e.
,
i.e.
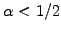 .
Although the superposition of advection and diffusion is slightly more
limiting, the overall conditions for numerical stability can conveniently
be summarized as
.
Although the superposition of advection and diffusion is slightly more
limiting, the overall conditions for numerical stability can conveniently
be summarized as
It is finally worth pointing out that a backward finite difference for
the advection is unstable for negative velocities 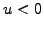 ; this defect of
non-centered schemes is sometimes cured with an upwind difference,
which takes the finite difference forward or backward depending on the
local direction of propagation (exercise 2.01).
; this defect of
non-centered schemes is sometimes cured with an upwind difference,
which takes the finite difference forward or backward depending on the
local direction of propagation (exercise 2.01).
SYLLABUS Previous: 2 FINITE DIFFERENCES
Up: 2 FINITE DIFFERENCES
Next: 2.2 Explicit 3 levels
![\includegraphics[width=4cm]{figs/FDe2lvl.eps}](s2img10.gif)


 ','..','$myPermit') ?>
SYLLABUS Previous: 2 FINITE DIFFERENCES
Up: 2 FINITE DIFFERENCES
Next: 2.2 Explicit 3 levels
','..','$myPermit') ?>
SYLLABUS Previous: 2 FINITE DIFFERENCES
Up: 2 FINITE DIFFERENCES
Next: 2.2 Explicit 3 levels
![]() and
no physical diffusion
and
no physical diffusion
![]() .
.
![]() using a
hamonic ansatz
using a
hamonic ansatz
![]() .
Define the amplification factor as
.
Define the amplification factor as
![]() ), the dispersion relation
(2.1#eq.3) shows that the 2 levels scheme is stable for
all wavelengths provided that
), the dispersion relation
(2.1#eq.3) shows that the 2 levels scheme is stable for
all wavelengths provided that
![]() ,
i.e.
,
i.e.
![]() .
Although the superposition of advection and diffusion is slightly more
limiting, the overall conditions for numerical stability can conveniently
be summarized as
.
Although the superposition of advection and diffusion is slightly more
limiting, the overall conditions for numerical stability can conveniently
be summarized as